UVA 13083
Name: Yet another GCDSUM
Link: https://uva.onlinejudge.org/external/130/13083.pdf
I did get the idea that I'll initially compute all the divisors of N using prime factorization & backtracking but I'm stuck in how to compute the gcd of the divisor pairs with a better complexity than O(n^2). Any help is really appreciated.











You can notice that the function is multiplicative. Thus, it is enough to think about the value of the function on the power of primes.
Do you see the formula?
Can you please provide a bit more hints?
Let f(·) be the function.
For a prime power pq, the divisors of pq are precisely of the form pk where 0 ≤ k ≤ q is an integer. Greatest common divisor of two divisors pk and pl is pmin(k, l). Therefore,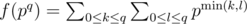 .
.
You can compute the above sum naively because q is small. An exercise: Describe a way to compute the above sum in O(q) arithmetic operations. In fact, the above sum can be computed even faster if I'm not wrong but this is not necessary here.
Can't we write F(pq) as F(p)*F(p)*...q times ? this will simplify things, or am I wrong about it ?
Did you even look at the sample output? f(2) = 5 and f(4) = 15. Clearly, 52 ≠ 15.
In general, for a multiplicative function f(·), f(xy) is not necessary equal to f(x)f(y). The definition of multiplicative function requires that x and y be coprime in order to satisfy the equation f(xy) = f(x)f(y).
ohh , I totally got it wrong there..
anta, is there any good approach to prove whether a number theoretic function multiplicative or not?
Ignore the below idea , it is incorrect
Once you see this function is multiplicative , you can prime factorize the number.After you have that then let's say the prime factorization is {(p1x1)*(p2x2)...}.Then the required ans is G(n)=G(p1x1)*G(p2x2)*.... *G(pnxn). The first term can then be written as G(p1)^x1 , now since p1 is prime G(p1) =GCD(1,p1)+GCD(p1,1)+GCD(p1,p1) = p1+2, from here on you can see the answer.
anta, meant to say that, since the function being multiplicative, we just need to compute the answers for prime powers only.
For doing that, I just used a simple "2 nested for loops". Consider n = p^a, some some prime 'p' and exponent 'a'. Now, if 'm' divides 'n', then it is of the form m = p^i, for 0<=i<=a.
Now, m1 and m2, we need to add their gcd to the answer, and we know gcd(p^i, p^j) = p^min(i,j). This is simply computed using "2 nested for loops"
As far as factorisation of number is considered, I used Pollard-Rho-Brent factorisation, having complexity of O(n^(1/4) log(n)). Also, since log(n) = 46, the nested for loops will not take much time as compared to the factorisation part. This solution of mine written in python3, gets accepted in 0.100 seconds.
For the source code, you can refer to Here .
If you have any doubts, you can ask below. Also, I found finding the formula for p^a tough, So I just wrote simple nested for loops which in this case is much smaller than factorisation which dominates time complexity.
Solution updated to single for loop.