AtCoder Grand Contest 005 will be held on Saturday (time). The writer is yosupo.
Let's discuss problems after the contest.
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 156 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | nor | 152 |
AtCoder Grand Contest 005 will be held on Saturday (time). The writer is yosupo.
Let's discuss problems after the contest.
| Name |
|---|



Never mind. I was wrong.
Actually it seems like there's a 15 minutes break between the contest.
rng_58 likes your icon, according to this comment.
It clashes with the ICPC Preparatory Series contest on Codechef. :(
I am really interested why all in top 10 are reds except semiexp whose color is green?Is it a bug?
Actually his color is #92D050. If you reach 3200, you can choose your own color (tourist and Petr haven't decided their colors though).
I hate FFT :( the modulo is friendly though
Anyway, nice problems!
The best thing about AtCoder is trying to read the Japanese editorial using Google Translate.
Edit: My bad, I see the English version now.
There's English editorial below Japanese editorial.
It would be much better to provide editorials in English and Japanese in separate file. I don't like seeing Japanese editorial at the top. Can something be done in this regards? Anyways, Thanks for great contests and well explained editorials.
Can someone explain the solution for D better? I'm lost at the Inclusion-Exclusion part (where did the sum come from)
Can someone please explain the editorial of D in a different way? I'm having some difficulty understanding it. How is that formula derived? And how to find M(k) in O(n^2) using DP?
Sorry for necroposting, but how to solve D in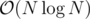 time?
time?
I think all you do is: notice that the only part of the editorial that needs O(N2) time is computing the Mk. You can compute all Mk for a single path of length l by straightforward combinatorics / dp.
Let Pl(x) be the polynomial where the coefficient of xk is the number of matchings of size k on a path of size l. Notice that in the graph, all paths are gonna be length l or l + 1 for some l (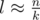 ). To find the overall Mk, this is equivalent to a convolution so you can just compute Pl(x) and Pl + 1(x) for the appropriate l and then raise them to the correct power and multiply. This can all be done by FFT in
). To find the overall Mk, this is equivalent to a convolution so you can just compute Pl(x) and Pl + 1(x) for the appropriate l and then raise them to the correct power and multiply. This can all be done by FFT in  ,
,
How do we compute Pl(x) in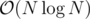 time?
time?
Say you have a path of length l. You want to pick k of the edges so that you don't pick any two adjacent edges. This is just a binomial coefficient, something like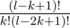 or something.
or something.
Oh, you are right. Thanks :)