Hello CodeForces Community! I would like to take this opportunity to invite you to take part in the third and last contest of IPC’s ICPC Preparatory Series. This will be the final chance for those who have been shortlisted in the previous rounds of the contest. As usual, there will be a mirror contest that will run in parallel with an hour delay. I hope you will grab this chance by taking part in the contest which will also be a practice for the ACM ICPC regional which are approaching quickly.
Joining me in the problem setting panel, we have: gvaibhav21 (Vaibhav Gosain), SameerGulati (Sameer Gulati), PrashantM (Prashant Mahesh), a0666 (Malvika Joshi), ashish1610 (Ashish Khatkar), jagsxi (Ayush Jaggi).
Contest details Time: 02th October 2016 (2000 hrs) to 03th October 2016 (0100 hrs). (Indian Standard Time — +5:30 GMT) — Check your timezone.
Contest link: https://www.codechef.com/IPC15FLC
Mirror Contest details: Link: https://www.codechef.com/IPC15CMR
Date: Sunday, 02th October 2016, 9:00 PM, IST. Check your timezone.
Duration: 5 hrs.
Note: This contest is open for the whole community.
Prizes: Cash prizes for the top three spots are declared after taking into consideration of the cumulative score (of the final 3 contests):
Global Category:
1st Prize: $1000
2nd Prize: $500
3rd Prize: $200
Indian Category:
1st Prize: INR 50,000
2nd Prize: INR 25,000
3rd Prize: INR 10,000
*More details about the preparatory series can be found here: https://www.codechef.com/ipc/2015 Good Luck! Hope to see you participating!!
How can I get solutions?
Here are my solution ideas for the first 6 problems.
LPALIN: Simple idea, if string is not palindromic originally delete everything expect a single character.
SURESH: Interesting question with a neat formula ((T[0] / P[0]) + T[1]) / P[1]...
Let Ri denote expected time to reach level N after completing i levels.
Ri = Pi·(Ri + 1 + Ti) + (1 - Pi)·(R1 + Ti)
For i = 2, R2 - R1 = P2·(R3 + R1) + T2
Manipulating R1, R1 - R2 = T1 / P1
Also, we know R_n = 0.
Putting value of R2 in R3, T1 / P1 = P2·(R1 - R3) - T2
which implies R1 - R3 = ((T1 / P1) + T2) / P2
We solve this recursively to get the formula.
MINWALK: Dijkstra to find shortest paths of all nodes from S, T and V. For all nodes, try to make that node the junction, where paths from all nodes will meet(and path from v->node and s->node will intersect).
SVENGY: Trivial DP works in O(N2), optimise it to O(N·maxval) where maxval = 103. Basically, exploit that you only need to check one of the indices in array if they have the same value.
ALTREE: Note that in resulting tree, all nodes have at most 1 edge of each color(because otherwise there will be path having alternate colors). This means that resultant tree is a chain. Do dynamic programming in O(2n·n + m) keeping state, (last, mask) where last is previous node added, and mask denotes nodes already in chain.
LINES: Fix one point and try all other points and store frequency of all slopes. Check if some value has greater than p·n / 100 occurrences. This is O(N2). Optimise using trick given below.
Can someone post the solution to the 2nd last problem, LBRACKET?
It can be solve by Segmentree where each node[L, R] we define cnt[0], cnt[1] are the number of '(', ')' respectively. Additionally, we define prefix_min (prefix_max) which is the minimal (maximal) sum prefix of segment[L, R]. Now, it's easy to flip an interval with lazy propagation. For query 2, we need to find the largest y such that sum[x, y] = 0 and node[x, y].prefix_min = 0. The easy way with complexity O(log(n)2) is using binary search. We can reduce it down to O(log(n)) with a bit of complication. Check my solution: link
Another method to solve SURESH is to consider E(i) as the expected time to pass i levels. Then we have the following recurrence:
Btw, why restrict the p_i values from [0.4, 0.6] and t_i from [1, 5]?
The reason for such constraint was precision. The output could be very large and may not fit into double's precision.
What is the solution of LINE problem??
I noticed many contestants using random shuffle and 300 as the upper bound of the points needed to be considered as center. Is there a proof for such an assertion??
Also some solutions don't even use random shuffle (just 300 as upper bound).
If there is a line contains at least p / 100 points. Randomly choosing a point, the probability it is on that line is p / 100.
for higher values of P , chances of any random point being a part of the optimal line are quite high , while for small value of P , say P = 1 , there will still be atleast N / 100 points on the optimal line , For N = 104 , chances of a point being a part of the optimal line are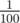
, so if we choose X random points , chances of atleast 1 point being a part of optimal line is 
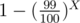which comes out to be around 0.950959... for X = 300 which is pretty good.
Thanks for this nice explanation, but does it follow even if we don't use random shuffle and just pick starting 300 elements of input ??
Can you move the problems to practice section.
Hi, the problems have been moved to the practice session.
Can there be more than one white edge between two vertices in alternating tree?
No.
It was a good contest.
How can we solve Luther and Brackets?
A brief editorial would be a lot useful.
https://discuss.codechef.com/questions/85765/lbracket-editorial
How to do the problem Save Energy in less than N^2?please explain
If you write cost function for path i->j->k and compare it with the cost function for path i->k you can see that the former is better (costs less energy) if and only if either |A[j]| < |A[i]| or |A[j]| = |A[i]| with A[i]>0.
From this observation it is quite easy to see that the optimal path would be greedy jumping from 0 to first i such that |A[i]| < |A[0]| or A[i] = -A[0] (if A[0]>0) or directly to n-1 if there is no such i and so on. Jumping greedily to n-1 solves the problem with O(N) complexity.
Nice one :) Due to the fact that cost function is good and we can split each jump into consecutive steps, we can also solve it in more straightforward way — by computing a DP[i][j] which will tell us smallest cost to reach position i while using some A[x]=j; now from position i we can either keep moving forward using same "old" value of A, or start using A[i]. Such solution works in O(N*cnt_A) where cnt_A is count of distinct possible values of A[i].
Can you post the code for your explanation ? It would help me understand your solution better. Please try and include comments wherever possible. Thanks ! Also, how did you go about calculating the two necessary conditions for this question ?
link to solution from the contest.
As for conditions you just straight out write both costs and after a short simplification you can see that path i->j->k is better than i->k if and only if Aj + (k + j)Aj2 ≤ Ai + (k + j)Ai2 which is holds when |A[i]| > |A[j]| or |A[i]| = |A[j]|, A[i] > 0.