vepifanov's blog

Intel Code Challenge Final Round (div.1 + div.2 combined) editorial
By vepifanov, 8 years ago, translation, In English
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
  • Vote: I like it
  • +92
  • Vote: I do not like it

Comments Comments (41)
| Write comment?
»
8 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Can you please elaborate soln. for problem C?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    The Ray will always move with a vector (1,1) or (-1,1) or (1,-1) or (-1,-1) because it always change its direction 90° and in a straight line. For every one of this lines, witch are all parallels to the diagonals, if you extend them to the infinite they only cut once the x axis. In fact, they cut the x axis in (x+y) if the vector is (1,1) or (-1,-1) and in (x-y) if it is (1,-1) or (-1,1). You can then calculate for every sensor this number for the both line that pass throughout it. You make then lists of sensors for each possible sum and difference of coordinates.

    You then simulate the ray, going from wall to wall in O(1), and checking and updating all the sensor that are in both lines that pass trough every point in the wall you touch.

    It's then O(N) with N being the number of sensors.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      It's also important to note that you only enter in a loop when you arrive to one of the other three corners (0,N), (M,0) or (N,M).

      → Reply
»
8 years ago, # |
← Rev. 4   Vote: I like it -36 Vote: I do not like it

Another idea for Problem A without setting many conditions! 21324550

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Pretty cool! Could you explain for nubbie please)?

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      of course, you just try the first day in the input with the months {28, 30, 31} and simulate the cycle till the second day in the input matches or else output NO!

      → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

That solution for C was so easy! I tried to elaborate a mathematical solution but things got too complicated. BTW, is it possible to get time for each point in O(1)? It's pretty easy to convert time into coordinates, so there basically must be a way to do the opposite i.e. convert coordinates into time.

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I doubt that O(1) solution exist, but here I describe idea for O(log(n+m)) solution: http://codeforces.net/blog/entry/47598#comment-319789

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I agree with you.We need binary search to solve it.So it is log(n+m)

      → Reply
    • »
      »
      »
      8 years ago, # ^ |
      ← Rev. 2   Vote: I like it -10 Vote: I do not like it

      21286454 is O(1) for each query for problem C

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it +22 Vote: I do not like it

        Lolwhat. It obviously uses Euclidean algorithm, which definitely has logarithmic complexity. O(1) solutions rarely use 'while' cycles, I should say:)

        → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it +3 Vote: I do not like it

        Oh, I'm sorry, it seems you are right. I didn't notice that we only need to compute gcd and corresponding coefficients only once.

        → Reply
        • »
          »
          »
          »
          »
          8 years ago, # ^ |
            Vote: I like it +6 Vote: I do not like it

          Yeah, I think people misunderstood my statement. I should have clearly mentioned. O(1) query time. Preprocessing is O(log(n+m))

          → Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 4   Vote: I like it 0 Vote: I do not like it

    21347465 is my Accepted code using Chinese Remainder Theorem. I think it is O(1) though not completely sure.
    21286454 is definitely O(1) query time, written by eatmore

    → Reply
»
8 years ago, # |
  Vote: I like it -16 Vote: I do not like it

there are on subtrees of size k at all

Maybe there's a typo, it should be

there are no subtrees of size k at all

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I just can't understand why I get downvote. Or that we shouldn't point out typos?

    → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can problem D be done using this approach: starting from index 1, for each window of length 'm', we find the smallest character and add it to the answer. For checking the smallest character, set can be used with the element stored being (character,index). As we move the window, we remove the first element of the previous window and insert the new element of current window, then check if the new smallest character is the same as previous. If it is not, we can add it to our answer. Let the answer be 'ANS'.

At the end, we can iterate through the string and for each character that is not added in the answer, check whether it is less than the largest character that exists in 'ANS'. If yes, we can add it to answer and continue.

→ Reply
»
8 years ago, # |
  Vote: I like it +8 Vote: I do not like it

The Tutorial of problem F use status O(n*n*d).But many people solve F with status O(n*d).Can anyone tell me how to solve it with status O(n*d)?

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

If i-th bit is equal to one for at least one vector of the basis, then this bit will be equal to one in the 2^r - 1 triples.

Can you explain why?

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 5   Vote: I like it +19 Vote: I do not like it

    Fix vector u in the basis which has i-th bit. Not depending on vector v from first 2^{r-1} vector, one of v and v xor u will have 1 and other one will not

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      in know it's been long .. but can u explain the basis related part of G in simpler terms

      → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can anyone explain D?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    it is important to observe that if a letter L is needed then all the occurrences of the letter from 1..L-1 will be included in the lexicographically smallest string. Now the main problem is to find the least number of occurrence of the letter L.

    The initial problem is to find the max smallest letter L within which we will be able to visit all the intervals. To do this, we will iterate through all the intervals for each of the letters. In each iteration we will check whether the current letter indexes can fill any intervals and mark them. While doing this we will have to make sure that we always take the right most position and if we can use that position in other interval then we have to use it as it will solve our main goal of taking the least number of occurrence of the current letter. See the below test cases for clarification.

    test case: 3 aaaaaaaaa ans : aaa

    3 ababab ans : aa

    → Reply
»
8 years ago, # |
  Vote: I like it +5 Vote: I do not like it

Anyone solved 'D' with segment tree?

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can anyone explain, why cycles with "zero" XOR sum makes sense for answer? I have submission 21335792, where I ignore all "zero" cycles, it gets WA24. But here 21335866 I use all cycles, even "zero", and get AC.

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it +3 Vote: I do not like it

    The mistake you made wasn't ignoring the "zero" cycles but "int mr = min(sz, 60)"

    notice that mr may be larger than sz

    what if cyc = {1, 4} ?

    You will get mr = 2, base = 1, r = 1 but it should be that mr > 2, base = 5, r = 2.

    So just change it to "int mr = 60;" and everything will be right.

    → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

"cut(i, j) = min(cut(i - 1, j - 1) + si, cut(i - 1, j) + pi + j * m)."

In problem E, what do you mean by m? I can solve the problem in O(n^3) but don't understand this relation.

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    They meant c, maximum amount of goods for a single transportation. So they cut all edges to j cities, which are currently in set A.

    → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    You consider two cases. If you assign the ith vertex to set A, the capacity increases by si. Instead, if you assign ith vertex to set B, capacity of cut increases by pi+j*m. The j*m value comes from the j vertices in set A such that there is edge from those to ith vertex.

    → Reply
»
8 years ago, # |
  Vote: I like it +5 Vote: I do not like it

The 724E - Goods transportation can be also solved using greedy (didn't get this right during the contest). It's a little tricky, but basically you first do all the trading that doesn't require sending things, so that each city either just produces or just consumes, and then go through the cities from left to right. You can maintain a list of already seen and active "producers", along with an information on how much can each of them send if a "consumer" comes (either directly, or via other already seen cities that don't produce, but can be used to transfer goods through them). When you get a "consumer", greedily use producers, starting from the rightmost one.

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    "via other already seen cities that don't produce, but can be used to transfer goods through them"

    Can you please explain this a bit more?

    → Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

To problem E: why isn't it cut(i,  j)  =  min(cut(i  -  1,  j  -  1)  +  si,  cut(i  -  1,  j)  +  pi  +  min(j  *  m, si)) ? it also seems OK..

For the case that I cut both si and pi

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

editorial for problem F The number of trees that have exactly one centroid is equal to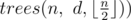

when n is even, it should be tree(n, d, n/2 — 1) to avoid counting 2-centroid cases.

→ Reply
»
8 years ago, # |
  Vote: I like it +5 Vote: I do not like it

I've found O(n*log(n)) solution for problem E and it ran in almost no time 21622504.

I felt that the constraints should have been higher but they were not...

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Eh, could you please explain your solution ?

    I am only able to solve the problem with the complex O(n2)

    Thx.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Instead of the approach given in the editorial we can do the following: Let the partition of vertices for the minimum cut be (S, V-S). Then |S| can take values from 1 to n+1. By doing some work it is easy to find out the capacity of the minimum cut which has |S| = i for i=1 to n+1. Our answer is evidently minimum of all these capacities.

      Have a look at my code after you brainstorm on my point given above...

      → Reply
»
8 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

In problem E, why the formula to calculate the minimum cut is ?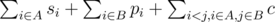

(Sorry if this is something trivial, I'm completely newbie in minimum cut problem)

→ Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Cut edges are saturated in max flow.

    → Reply