dead_lock's blog

A Problem on Vectors
By dead_lock, history, 8 years ago, In English

We are given a set V of distinct binary vectors {v1, v2, ...vn} each of size k.
Now you are free to chose a subset of V, SV = {vi1, vi2, vi3, ..., vim} such that

  • 1 ≤ i1 < i2.... < im ≤ n.
  • No two rows should be same in the kXm matrix M = [vi1vi2...vim]

We need to minimize m (the size of subset SV). (ie the columns of M)
For eg: a vector v of size 3 can be [0, 0, 1]T or [1, 0, 1]T and 6 more are possible.

  • Vote: I like it
  • +15
  • Vote: I do not like it

»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

What are the constraints?

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    1 ≤ n, k < 10
    But I was looking forward for the best complexity.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Let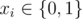 denote whether we take vi or not. For each two pairs of rows, among all the positions where any two vectors differ, we need to take at least one of such vectors. That is, for each two pairs of rows we obtain a constraint of the form 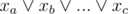. The valid solution then is defined by the AND of all constraints, which is a CNF formula. Solving CNF formulas is NP-hard, however this one is very simple — there are no negations. Therefore we can set for example, all xi = 1 (which is obvious even from the statement).

      On the other hand, we need to find minimal solution. And this becomes hard again, since it becomes a set cover problem (universe is all pairs of rows or equivalently a clause in the CNF formula, and the sets are given from each xi as a set if clauses which contain xi).

      The only difference from general set cover is that the pairs are related. But I don't think that these relations are enough for polynomial algorithm to be possible.

      → Reply