Tobby_And_Friends's blog

Segment Tree Problem from SPOJ, SEGSQRSS — Sum of Squares with Segment Tree
By Tobby_And_Friends, history, 8 years ago, In English

Problem Link: http://www.spoj.com/problems/SEGSQRSS/

While I do understand that the merge operation can be deduced from the equation (a + b)^2 = a^2 + b^2 — 2ab I could not specifically figure out how would I formulate the merge operation. Any help is really appreciated.

  • Vote: I like it
  • 0
  • Vote: I do not like it

Comments Comments (4)
| Write comment?
»
8 years ago, # |
← Rev. 4   Vote: I like it +1 Vote: I do not like it

First of all we need to think that what information we need to store in our Segtree. So we need to store two information in the segtree one is the sum of the squares of the numbers and the other is the sum of the numbers.Now why sum of the numbers ?? The reason is in the second update .The merge operation for the question is pretty direct just add the values of the child nodes to get the values of the parent node.

For this particular questions there are two types of updates :-

  • Set all the numbers same in a range. Its an easy one because in this the sum of squares of the numbers and the sum of the numbers can be directly computed the by the formula

Sum of Squares Of Numbers = (E-S+1)*NUM*NUM

Sum of Numbers = (E-S+1)*NUM

  • Now in the second update we need to increment all the elements within a given range. So here the tricky part is to calculate the sum of squares of the numbers after the update at some node in the segtree.

Sum of Squares of Numbers = Sum of Squares of Numbers before the update + (E-S+1)*1 + 2 *(Sum of Numbers Before the update)

Sum of Numbers = Sum of Numbers before the update + (E-S+1)

The above formula comes because let's say the numbers were a1 , a2 , a3 before the update so the sum of squares would be

a1*a1 + a2*a2 + a3*a3

Now after the update the sum of squares would be

(a1+1)*(a1+1) + (a2+1)*(a2+1) + (a3+1)*(a3+1)

which when you will expand will become

a1*a1 + a2*a2 + a3*a3 + 3*1 + 2*(a1+a2+a3)

So similarly we can do the same for more number of numbers . The rest part for this question is Standard Lazy Segtree Implementation.

→ Reply
»
8 years ago, # |
  Vote: I like it +1 Vote: I do not like it

That information alone is enough to solve the problem. Consider a range [l, r]. Sum of squares of that range is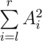 . Now suppose you add x to that range, the sum of squares now becomes 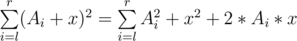. We can express that as 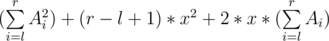. So if we keep the sum of squares as well as the normal sum for every range, we can process queries without a problem, you just need to be careful with the lazy propagation, specially with the set queries.

→ Reply
»
8 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Should I storage time of each update?

My solution needed to create two arrays lazy one for the first update and the other for the second update also store all the time for update ..... my soultion get AC , However I think test cases are very weak and my code is not right

my code

sorry, for my english is poor

→ Reply