Nams's blog

Edit Distance Problem in less than O(n^2) time
By Nams, history, 8 years ago, In English

I recently encountered a problem in a contest.It was very similar to edit distance.Only difference was that we are also given cost of each of the operation insert,delete and replace .We have to find minimum cost to convert string1 to string2. This problem is fairly standard and can be solved using dynamic programming in O(n^2) time. The problem statement for Edit Distance can be found here: Problem

But the constraints given in the contest were n<=100000 so larger test cases won't pass in O(n^2). So is there any way to bring the time complexity of the solution?

  • Vote: I like it
  • +3
  • Vote: I do not like it

»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

You can do it in O(N * K) where N = length of the string and K = maximum possible 'distance'.

→ Reply
»
8 years ago, # |
  Vote: I like it +8 Vote: I do not like it

Probably one of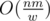 algorithms could pass (where n, m are lengths of the strings and w is the size of processor word). For example, see "A Fast and Practical Bit-Vetor Algorithm for the Longest Common Subsequence Problem".

→ Reply
»
3 years ago, # |
  Vote: I like it 0 Vote: I do not like it

can you share the problem link?

→ Reply