How to solve K, C?
→ Обратите внимание
До соревнования
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
5 дней
Зарегистрироваться »
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
5 дней
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 156 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | nor | 152 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 25.11.2024 12:00:50 (h1).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











How to solve L?
First, check what if a = 0 or c = 0
then if b is max and it's equal to F_{i+1} then D = b2 - 4ac = (Fi + fi - 1)2 - 4fifi - 1 = (fi - fi - 1)2 that is usually greater than 0, and zero if fi = fi - 1 i.e i = 2
otherwise D < 0 and there's no solutions.
fi2 - 4fi + 2fi + 1 < fi2 - 4fifi < 0
fi2 - 4fi + 1fi - 1 = fi2 - fi + 1fi - 1 - 3fi + 1fi - 1 = ± 1 - 3fi + 1fi - 1 ≤ - 2 < 0
C: можно заметить, что x очень быстро циклится (а именно, 90754 сравнимо с 1 по модулю 2333333). Потому T совпадает для вершин, идущих через 6 (за исключением, возможно, некоторого префикса и суффикса) и вообще веса рёбер совпадают с небольшим периодом. Исходя из этих соображений можно догадаться, что ответ в некотором смысле периодичен. Естественней всего ожидать периодичности последовательности разностей соседних ответов. Посчитав несколько её первых членов (для любого seed), можно заметить, что она действительно периодична с периодом 9 и небольшим предпериодом, что позволяет как угодно посчитать ответ для маленьких n, а потом воспользоваться периодичностью.
K: давайте переберём, какой НОД d всё-таки будет получаться. Тогда можно выделить числа из нашего массива, которые делятся на d, они разобьются на подотрезки исходного массива, на которых можно решать задачу независимо. Поделим все числа на отрезке на d, тем самым сведёмся к задаче, где НОДы на выделяемых отрезках должны быть 1.
Эту задачу можно решать так: сперва с помощью двух указателей и sparse table найдём для каждого r наибольшее такое l ≤ r, что НОД на подотрезке [l, r] равен 1 (или - 1, если такого r нет) — назовём этот массив
from[r]. Тогда максимальное число отрезков разбиения можно найти какans[r] = max(ans[r - 1], (from[r] == -1 ? 0 : ans[from[r]] + 1)(либо не берём последний элемент, либо берём, но тогда нет резона брать его в отрезке, который не минимальной возможной длины — ответ это не улучшит).Заметим, что ans автоматически получается отсортированным. Тогда число способов получить максимальное число отрезков разбиения можно пересчитывать так:
(смысл состоит в том, что либо мы не берём текущий элемент, либо мы берём его вместе с отрезком, на длину которого наложены ограничения — его левая граница должна быть не больше
from[i]и не меньше первого такого l, чтоans[l] = ans[i] - 1(так какansвозрастает, то для левой границы из этого отрезкаansкак раз равенans[i] - 1и в силу определенияfrom[i]мы действительно убираем справа отрезок, НОД на котором единицен.Асимптотика есть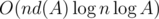 , где A — ограничения на максимальное число в массиве, d(A) — наибольшее число делителей среди чисел ≤ A, но плохой тест придумать не очень просто (например, если все числа равны числу с максимальным числом делителей, то подсчёт НОДа работает за O(1) и время работы получается
, где A — ограничения на максимальное число в массиве, d(A) — наибольшее число делителей среди чисел ≤ A, но плохой тест придумать не очень просто (например, если все числа равны числу с максимальным числом делителей, то подсчёт НОДа работает за O(1) и время работы получается 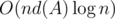 ). Зашло приблизительно за 1 секунду.
). Зашло приблизительно за 1 секунду.
В К можно решать задачу параллельно для всех d, тогда при фиксированной правой границе интересны лишь отрезки, для которых меняется gcd, а таких не более log A, итого у нас получилась асимптотика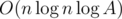 .
.
Я не уверен, что это можно объяснить, но код тут (работает 0.6)
В целом, у нас динамика вида dp[d][r] = {ans, cnt} — gcd всех отрезков равен d, последний заканчивается в r, ans — максимальное кол-во отрезков, cnt — кол-во способов. Только храним сжато и еще насчитываем префикс суммы, чтобы пересчитывать динамику
У нас были проблемы с тем, чтобы упихать это в МЛ. Пришлось руками считать длины всех векторов, ресайзить, сжимать неиспользуемые числа и т.д. Этого можно избежать как-то?
у нас тоже был МЛ. Мы не стали выделять память для тех d, которые ни разу не встретились, а выделять лениво при первой необходимости (см. комменты в коде выше) и это зашло за 150Мб.
Мы клали в
unordered_mapтолько встретившиеся пары (gcd, l), зашло без проблем.Да. Можно решать для каждого gcd за количетсво начал в которых можно получить такой gcd. Работает 1.3, с памятью проблем не было (80 метров) Вот код.
Which C? It is better if organizers do not name different tasks with same letters.
Как делать D? Какая идея? И если есть структура, какой структурой пользовались, если можно поподробней)
Расскажу про левую часть, правая часть делается точно так же
Основная идея: перейдем от записи a[i] — a[j] >= i — j к записи a[i]- i >= a[j] — j. Построим дерево отрезков на минимум по величине a[i] — i. Тогда на запрос для дома с номером buidling отвечаем так: находим ближайший слева разрушенный дом (при помощи, например set) — называем leftBuidling. Дальше ищем минимум на отрезке от leftBuilding + 1 до building — 1, если он меньше a[building] — buidling — рушим этот "минимальный" дом и продолжаем поиск, иначе прекращаем поиск.
Аналогично решаем для правой части (там будет a[i] + i)
У нас такая же идея была, но ва3, думал неправильно придумали) Но у нас ДО возвращало вектор, то есть все дома на отрезке неразрушенном, потом мы ловербаундом находили дома, которые разрушатся волной и разрушали их. Спасибо за ответ, пошел искать баги)
G. How did you solved it?
After splitting to sentences I tried to grep them with regex, but got TLE 29 (ideone).
Then tried use hashes, but failed on TC#3 (give a hint). Can't overcome it in two ways: 1) take each sentence as a hash key, which value is a hash of lowercased words;(ideone) 2) each word from sentences is lowercased and is a hash key, which value is an array of indices of an array of sentences.(ideone).
Later improved(maybe) regex solution with lookaheads, but there is no Upsolving for Div.2 :/ to test if it pass time limits (ideone).
Как Б решать? Мы сдали что то типа рассматриваем только точки, отстоящие от границ квадрата не более чем на 800, может ктото по другому решал?
Дело в том, что у треугольника с максимальной площадью все вершины будут лежать на выпуклой оболочке. Только что в дорешку сдал такое: Строим выпуклую оболочку, перебираем всевозможные тройки вершин, берем лучшую. Точек на оболочке мало, где-то порядка 30-50.
На самом деле задача решается за линию без предположения о случайности тестов "тремя указателями". Такая задача была в Петрозаводске лет пять назад.
А можно немного подробней узнать, как тремя указателями за линию решать?
http://codeforces.net/blog/entry/4136?locale=ru#comment-84282