sometimes I saw — unfortunately, I can't remember where I saw that — problems like below. I simplified the statement for clarity.
Problem)
You're given an array A with N elements, (A[0], A[1], ..., A[N-1]). and there are two kinds of queries
1 x y : change A[x] to y
2 l r : count the number of different elements in A[l], A[l+1], ..., A[r].
Condition)
1<=N, Q<=100,000 (Q: total number of queries)
1<=A[i]<=10^9 + 9 (A[i] : integer)
I tried to approach with segment tree but still have no idea.. How can I solve this kind of problems?











Auto comment: topic has been updated by nyan101 (previous revision, new revision, compare).
Auto comment: topic has been updated by nyan101 (previous revision, new revision, compare).
There is offline solution. Algorithm MO.
Mo's algorithm.
1 sort the query as follows.
(1) increasing order of l(i)/sqrt(N)
(2) if l(i)/sqrt(N) is same, increasing order of r(i)
2 start with L=R=0 and for each l(i), r(i)
(1) move L->l(i), R->r(i) and count.
(2) save the answer of the query.
total time complexity is O(Q log Q + N sqrt(N)).
Other solutions here only solve offline version, but it's not enough since his problem has updates. I heard of a way to do Mo's algorithm with updates, but if I don't quite remember how to do it (and it certainly isn't explained in the other comments :P)
I will describe one way to solve this problem in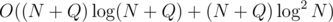 time. First, compress all the elements in A and all the queries to the range 1, 2, 3, ..., N + Q.
time. First, compress all the elements in A and all the queries to the range 1, 2, 3, ..., N + Q.
Let's create an array B. Bi contains the first index j such that i < j and Ai = Aj, or ∞ if there is no such index. That is, it is the first index to the right which is equal to this element.
Now, also create N + Q BBSTs. The ith BBST should contain the indices of all the elements whose value is equal to i.
We should now create segment tree on B. If a node in the segment tree is responsible for the range [i, j], then it should contain a BBST with all the elements Bi, Bi + 1, Bi + 2, ..., Bj. Note that you cannot use C++ set for this, you must implement your own.
Now let's look at how to answer the queries.
You can try implementing it here: UVa 12345 — Dynamic len(set(a[L:R]))
for the definition of array B, is the condition Bi = Bj ? instead of Ai=Aj? Thank you so much for the detail explanations
Sorry, it's a typo. I've fixed it.
uh... what about i>j and "it is the first index to the right ~". sorry but my English skill isn't enough so I'm confused between i>j and i <j. (is i <j right?)
Edir: Nevermind. I got it
You haven't used the N BBSTs in second query, right?
If you need it in the first query to change Bx to the appropriate element (and also first index to the left of x which is equal to Ax), then it can also be done with a simple array, isn't it?
So where are we using the N BBSTs?
Yes, the BBSTs are only for the first query.
I'm not quite sure how you can guarantee runtime per query using only a simple array. Maybe you can explain your approach for it, but I figured the BBSTs approach was the simplest. :)
runtime per query using only a simple array. Maybe you can explain your approach for it, but I figured the BBSTs approach was the simplest. :)
Can someone please explain what this is? I haven't seen any way to do this myself. Wouldn't Mo's require a static array for processing queries offline? Thanks :)
A red coder posted this as a comment a few months back. I have not implemented it myself and I don't really understand the idea behind it, but he is red, therefore he must be correct ;)
The runtime is somewhere around O(N5 / 3), though, which is cutting it pretty close considering this probably has some constant factors. The benefit is that it can be used in other situations where Mo's algorithm is the only solution.
http://www.spoj.com/problems/DQUERY/
Simple version.