Hi,
I'm solving this POI problem: http://main.edu.pl/en/archive/oi/15/kup . Basically, given an integer k(1 ≤ k ≤ 109) and an N by N square grid(1 ≤ N ≤ 2000) of non-negative integers, you have to find some rectangle in the grid such that its sum is between k and 2k, inclusive.
I can come up with O(n3) solution using prefix sums and monotonicity, however to make the problem fit the time limit I need something faster. By google translating the editorial, I think it's divide and conquer, but I couldn't understand the details as the translation was very bad. I would appreciate any help on this problem :D
Here is an idea I came up with, but I didn't code it and submit it yet.
First,you should get rid of numbers bigger than 2k (by marking them as -1 for example) because they will never be in the answer. Also, if there is any number in the range [k,2k] then this is the answer. Now we have ended with a grid of numbers from 1 to k-1. Suppose that we are only dealing with a 1D grid then for each index i we must find the maximum index j to its right such that there is no -1 in the segment [i,j] now if the sum of values in this range let's name it s is more than 2k (if it is less than k we should skip it / if it is in the range [k,2k] then it is our answer) then there must be a subsegment of segment [i,j] such that it is our answer.Why this true? Because at some index x such that i<=x<=j the sum s became more than 2k and since all values are less than than k(we have 2k<s and a[x]<k) then 2k-a[x]<s-a[x]<2k then k<s-a[x]<2k and s-a[x] is the sum of elements in segment[i,x-1].
We can do the same for the grid for each row we compute the same values(find the maximum j) as it is a 1D array. Then we try to expand the segment we found upward and the downward we can use binary search to do that and end up with an O(n^2*log n) .I have an idea to optimize it to O(n^2) but it is not necessary.
Are you sure about the complexity analysis? I thought of the same solution, but it seems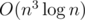
to me. Aren't you doing 
work per row? If not, can you please explain in some more detail. Thanks.
No O(n*log n) per row we don't try every possible segment in each row. We deal with each row as a 1D array and try to expand the segment [i,j] upward and downward until we find the answer.
There is a neat N^2 solution. If there are numbers in suitable range, print them. Bigger numbers can't be used of course. This is the first step.
Later, we'll use the standard largest area rectangle finding algorithm (the one with stack) to find any rectangle with size > k. Then, do this:
if(rectangleOK()) output it. Divide rectangle in two parts — this way at least one part has size > k. Perform the algorithm recursively on it.