С 9 по 12 января 2017 года будет проходить областная олимпиада по информатике. Первый тур олимпиады состоится 10 января, второй — на следующий день. Постараюсь разместить здесь условия и решения задач как можно скорее, естественно не раньше начала самих туров :) В комментариях предлагаю обсудить задачи, поделиться идеями по поводу их решения, мыслями...
Всем участникам желаю удачи!
UPD. Первый тур завершен. Ниже можно почитать, как же получить полные баллы по задачам.
UPD2. Второй тур тоже завершен. Можно почитать разбор, кроме последней задачи — я ее не решал, да и решений можно придумать множество.
Первый тур
Задача 1
Отсортируем пары (ai, bi) по возрастанию ai. Возьмем первые K подарков. Сложность решения: O(N·log(N)).
Задача 2
Кому может быть выгодно заполнить индивидуальную декларацию? Очевидно, что если жителю с доходом x выгодно заполнить декларацию, то и жителю с доходом y < x будет выгодно заполнить декларацию. Поэтому отсортируем исходный массив в порядке возрастания. А дальше проверяем, выгодно ли каждому жителю заполнить декларацию. Если жителю невыгодно заполнить декларацию, тогда для этого жителя и всех остальных задаем среднее значение. Выводим ответ. Итоговая сложность O(N·log(N)).
Задача 3
Следующее решение я не доказывал, так что будет интересно почитать доказательство (или опровержение) в комментариях.
Заметим, что на самом деле нам достаточно сделать min(n, k) операций. Теперь реализуем простейший алгоритм: будем заменять самый частый символ на самый редкий. Такое можно реализовать за время O(min(n, k)·26). Но на этом еще не все. Такой алгоритм некорректно сработает на строке abbbbbb. В таком случае выгоднее избавиться от символа a. Поэтому отсортируем наши символы по количеству вхождений в строку S и просто переберем, какие же символы может содержать строка. Ну а дальше находим ответ для каждого случая. Итоговая сложность: O(n + min(n, k)·262).
Задача 4
Научимся находить ответ для определенной вершины. Для этого подвесим дерево за эту вершину. Для каждой смежной вершины посчитаем такую таблицу: f[i][j] — количество путей четности i и баланса j. Под балансом будем понимать сумму + 1 и - 1 — для вершин с большим номером и вершин с меньшим номером соответственно (по сравнению с номером корня дерева). Такую таблицу можно посчитать одним проходом поиска в ширину.
Как же найти ответ для выбранной вершины? Для этого нужно рассмотреть 2 случая:
- Вершина является концевой в пути, тогда к ответу прибавим: 2·f[0][0];
- Вершина является промежуточной, тогда к ответу нужно прибавить 2·f1[i][j]·f2[i][ - j], где f1 и f2 — матрицы f подсчитанные для смежных вершин, через которые проходит путь.
Если аккуратно объединять ответы для смежных вершин, можно добиться асимптотики O(N). Соответственно для N вершин итоговая сложность O(N2).
PS. На самом деле, можно не хранить четность вершины, так как это показывает баланс.
Второй тур
Задача 1
Нужно отсортировать числа исходного массива в порядке возрастания. Ответ найдем по формуле: 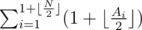 . Сложность решения: O(N2) или O(N·log(N)).
. Сложность решения: O(N2) или O(N·log(N)).
Challenge. А можете ли вы решить за время O(N) ?
Задача 2
На мой взгляд самая неприятная задача, но не сказал бы что сложная... Можно решить разными способами, но я расскажу вкратце свой способ.
Суффиксом длины i я буду называть младшие i бит числа N. Воспользуюсь такой динамикой: f[i][j][k][l] — количество вариантов чисел длины i, если последние j бит равны l и число меньше суффикса (при k = 0) или больше суффикса (при k = 1). С помощью такой динамики можно найти ответ за время: O(402·22). Рекуррентные формулы я писать не буду, так как они получаются довольно громоздкими (я уже говорил, что эта задача мне показалась не самой приятной), но их можно посмотреть в моем решении, ссылку на которое я оставил ниже. Итоговая сложность: O(1).
Задача 3
Пусть у нас числа a и b — элементы массива, дающие оптимальный ответ. Представим их в таком виде: a = x·y1, b = x·y2. Тогда, если gcd(y1, y2) = 1, то lcm(a, b) = x·y1·y2. Переберем x, а в качестве y1 и y2 будем брать первых два минимальных частных от деления 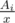 . Перебирать все делители можно за
. Перебирать все делители можно за 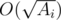 . Получим итоговое решение за время:
. Получим итоговое решение за время: 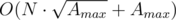 .
.
Задача 4
Задача на открытые тесты. Нужно было написать какой-нибудь алгоритм с учетом того, что все веса являются степенями тройки.
Результаты
Спасибо markysha и kodek за то, что поделились результатами областей.










