ed1d1a8d's blog

Non-Decreasing Array Problem
By ed1d1a8d, history, 8 years ago, In English

Here is a problem my friend smurty posed:

Say we are given an array of non-negative integers of length n, representing stacks of dirt of certain heights. We can move one piece of dirt from one pile to an adjacent pile for cost 1. What is the minimum cost it takes to transform this array to be non-decreasing?

Neither me nor my friend could come up with a polynomial time solution in n to this problem. Can CF think of something?

EDIT: BUMP

  • Vote: I like it
  • +43
  • Vote: I do not like it

»
8 years ago, # |
  Vote: I like it -26 Vote: I do not like it

I have seen several problems of that kind, but the root one (at least for me) is problem E from NWERC 2008 problemset. It's a generalization of yours, and still the solution is polynomial :)

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +20 Vote: I do not like it

    These problems hardly have anything in common.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it +20 Vote: I do not like it

      I must concur with Noobgam. The setup of the problem is similar, but I don't see how one can easily transition the cost function from that problem to this one. That is the main difficulty with this problem in my opinion.

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it +10 Vote: I do not like it

        Ok, my bad :(

        Maybe this could be useful:

        If the original array is a1, a2.. , an, then define A0, A1 .. An as the sum of the corresponding prefix of the original array (with A0 equals to 0).

        Then the conditions of the problem translate (in array A) to:

        • You can add 1 or substract 1 from any Ai with i > 0 or i < n with cost 1.

        Your objective is to transform the array A to a non-decreasing convex array with the minimum cost.

        I have come up with some neat conclusions from that, but no real solution :(.

        Another possibility is that this problem is somehow equivalent to knapsack, as it can be solved with dynamic programming too(making a pseudo-polynomial solution easy, not a polynomial as the question requires).

        → Reply
»
8 years ago, # |
  Vote: I like it +9 Vote: I do not like it

Waiting for someone to reply

→ Reply
»
8 years ago, # |
  Vote: I like it +5 Vote: I do not like it

Isnt this solved by performing a count of how many changes in a merge sort ? I mean, merge sort is going to shuffle adjacent numbers. So if you count the number of changes, maybe this will be the best answer. I can't prove that is true, can someone help ?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    The best solution does not necessarily preserve the heights. For instance, if we had two piles: 4 2 -- the best thing to do is move one dirt pile to the right and turn it into 3 3. Sorting would not get you this solution.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it +5 Vote: I do not like it

      Oh well, I completely miss understood the problem. :D

      → Reply
    • »
      »
      »
      8 years ago, # ^ |
      ← Rev. 3   Vote: I like it 0 Vote: I do not like it

      Please add this sample test to the problem to well understanding!

      → Reply
»
7 years ago, # |
  Vote: I like it +15 Vote: I do not like it

@ed1d1a8d did you come up with a solution to this problem? My best algo currently is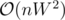 (maybe could be improved to 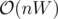with some simple optimization trick) where W is the sum of the heights.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +15 Vote: I do not like it

    I do not know of a solution not dependent on W.

    → Reply