What is the time complexity for Miller Rabin Primality Test?
Here is the algorithm from wikipedia page.
write n − 1 as 2^r·d where d is odd.
WitnessLoop: repeat k times: //runs k times.
{ pick a random integer a in the range [2, n − 1]
x ← a^d mod n
if x = 1 or x = n − 1 then
continue WitnessLoop
repeat r − 1 times: //r=O(logn)
{
x ← x^2 mod n //TC=O(logn)
if x = 1 then
return composite
if x = n − 1 then
continue WitnessLoop
}
return composite}
return probably prime
According to me the worst case time complexity would be O(k*(logn)^2)? But the wikipedia page mentions it as
O(k*(logn)^3). Can anyone help me out?
https://en.wikipedia.org/wiki/Miller%E2%80%93Rabin_primality_test
The complexity of multiplying two big numbers in a naive way is square of the length of these numbers. So I think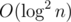
x ← x^2 mod nshould beWe generally multiply two big numbers numbers using the following method:-
It assumes that 2*c is in the range of long long.
long long mulmod(long long a,long long b,long long c)
{
long long x = 0,y=a%c; while(b > 0) { if(b%2 == 1) { x = (x+y)%c; } y = (y*2)%c; b /= 2; } return x%c;}
I think the complexity of this will be O(logb).
And in our case O(logx),as x=O(logn) so we can say it is O(logn).
Are you talking about how exactly multiplication is handled by the system?
By big numbers, I meant the numbers that can't be directly handled using native types(such as long long). According to my understand, the wiki is talking about this kind of numbers. Usually they are split into parts and saved in an array. For example if base=100, x=1234. Then the array may be a[0]=34, a[1]=12.
Multiplying two big numbers in a naive way looks like:
So the complexity is O(len2), which is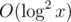
. By using FFT, the complexity can be reduced to 
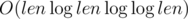, result the 
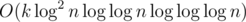in the wiki.
Just curious, in which cases would this be better than a root N brute force check? It seems that root N is about equal to log^2 N, and the test only tells you if the number is probably prime or not.
probability of wrong answer is 4^-k there k is number of iterations, so it is very small number when, for example k = 30. and for N = 10^18, root is 10^9, but log^3 is ~ 200000