You are given a sequence A1, A2, ... , An, - 1000 ≤ Ai ≤ 1000, 1 ≤ n ≤ 1000.
You can split this sequence into contiguous non-empty parts
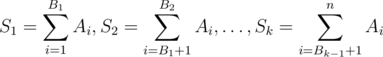 .
.
Your task is to find the maximum value 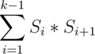 . If k = 1 then sum equal to 0.
. If k = 1 then sum equal to 0.
Can anyone help me come up with solution?











Let dp[n][len] be the maximum value I can get with the first n elements of the sequence if the length of the last block is len. It is easy to see the formula dp[n][len] = mink(dp[n - len][k] + (sn - sn - len) × (sn - len - sn - len - k) where si is the accumulative sum of the first i elements. Now dp[n][k] = mink(dp[n - len][k] + (sn - sn - len)sn - len - (sn - sn - len)sn - len - k dp[n][k] = mink(dp[n - len][k] - (sn - sn - len)sn - len - k)) + (sn - sn - len)sn - len the first part can be calculated using convex hull trick, the complexity will be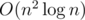
Btw is there a link to submit the problem??
http://codeforces.net/gym/101237/problem/F
In your question it is not clear whether you are given k or not. If you are not given k the solution provided by jcg will be correct. If you are given k the problem can be solved using the approach described here and here in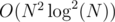 . But it can be further optimised to
. But it can be further optimised to 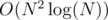 , because we can do convex hull (which we actually use inside the binary search) in O(1) time using a stack.
, because we can do convex hull (which we actually use inside the binary search) in O(1) time using a stack.
It seems that I reply to the correct statement.. In your version how you deal with the queries in the convex hull in O(1)? The values in the original sequence can be negative.