Всем привет!

Как вы, наверно, знаете доступ/добавление/удаление в хэш-таблице работает за O(1). Сегодня мы попытаемся улучшить эту оценку. Теперь рассмотрим реализацию хэш-таблицы с закрытой адресацией: пусть функция h равновероятно переводит каждый элемент множества A в множество B, те h: A → B, где A — множество возможных значений, а B — первые k натуральных чисел, для просты возьмем k = |A|. Если жи есть два элемента x, y для которых h(x) = h(y), то будем добавлять их в цепочку ячейки h(x) для разрешения коллизий. Вообще раз O оценка — это оценка сверху, то давайте далее полагать, что в каждую такую ячейку попадет t = 1 элементов. Тогда изменим способ хранения элементов со списка на set, но мы знаем, что время работы операций в set есть 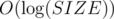, но так как размер нашей ячейки t, то операции работают за 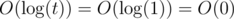, отсюда получаем, что n операции на нашей хэш-таблице отработают за O(n·0) = O(0).