arman_ferdous's blog

What is the time complexity?
By arman_ferdous, history, 8 years ago, In English

Recently I wrote this code to find the sum of all the digits of the number until the number turns into a one digit number. For example: number 567, we add all the digits and we get 5+6+7 = 18, now we add all the digits of 18 and we get 1+8 = 9. We can't add anymore digits because there is only one left and thus the result is 9.

Now I am having trouble figuring out the time complexity of this recursive code. Can anyone help?

int digSum(int n)
{
    if(n < 10) return n;
    return digSum(digSum(n/10) + n%10);
}
  • Vote: I like it
  • +9
  • Vote: I do not like it

»
8 years ago, # |
  Vote: I like it +22 Vote: I do not like it

It is . But this code is really strange. It works only because ans = 1 + (n - 1)%9.

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it +11 Vote: I do not like it

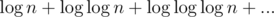    What's the reasoning behind it being ? Specifically, why is for all positive terms ?

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
      ← Rev. 2   Vote: I like it +5 Vote: I do not like it

      We know n + n/2 + n/4 + ..... converges to 2n. The log of the previous term means that the ratio between adjacent terms is always less than 2. Therefore your series sums to less than 2 log n.

      → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it +1 Vote: I do not like it

      It would be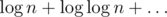 if it was written in a proper way like

      int getSum(int x)
{
    int sum = 0;
    while(x > 0) {
        sum += x % 10;
        x /= 10;
    }
    return sum;
}
int getRoot(int x)
{
    while(x >= 10) x = getSum(x);
    return x;
}

      But the code from post works in T(n) = T(n / 10) + O(1) which is obviously .

      → Reply