Educational Codeforces Round 20
By awoo, history, 8 years ago, translation, In English

Hello Codeforces!

On April 28, 18:05 MSK will be held Educational Codeforces Round 20.

Series of Educational Rounds continue being held as Harbour.Space university initiative! You can read the details about the cooperation between Harbour.Space and Codeforces in the blog post.

Here is the special message from Harbour.Space University for girls from India:

Harbour.Space University offers a unique opportunity to win a FULL SCHOLARSHIP for #womenintechIndia and join our amazing Data Science, Computer Science or Cyber Security Master's Programme in Barcelona, Spain!
Follow this link to complete the application form.

The round will be unrated for all users and it will be held with extented ACM ICPC rules. After that you will have one day to hack any solution you want. You will have access to copy any solution and test it locally.

You will be given 7 problems and 2 hours 15 minutes to solve them. Though this round may come a bit harder than two previous ones, we still hope that everyone will enjoy problems.

The round was prepared by Ivan BledDest Androsov, Mikhail MikeMirzayanov Mirzayanov and me.

Good luck!

UPD: Editorial is available here

Congratulations to the winners:

Rank Competitor Problems Solved Penalty
1 Um_nik 7 129
2 bmerry 7 160
3 kmjp 7 191
4 KrK 7 212
5 rajat1603 7 235

Congratulations to the best hackers:

Rank Competitor Hack Count
1 halyavin 135:-25
2 n.grechiha 20
3 oipotato 17
4 tqyaaaaaaaang 16
5 GreenGrape 16:-3

324 successful hacks and 209 unsuccessful hacks were made in total!

And finally people who were the first to solve each problem:

Problem Competitor Penalty
A kmjp 0:02
B RockyB 0:02
C Lewin 0:07
D Um_nik 0:15
E eddy1021 0:20
F tanphatls987 0:07
G ODT 0:33

  • Vote: I like it
  • +178
  • Vote: I do not like it

Comments Comments (47)
| Write comment?
»
8 years ago, # |
← Rev. 2   Vote: I like it +17 Vote: I do not like it

Hope everyone enjoy the contest. :)

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by awoo (previous revision, new revision, compare).

→ Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it -12 Vote: I do not like it

。

→ Reply
»
8 years ago, # |
  Vote: I like it +22 Vote: I do not like it

The duration in Contests list is 2 hours.

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

What is time complexity needed for acc on C? I can't belive didn't passed.I found all factors of n in and got sorted array.It's easy to see that gcd|n and 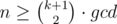so we need to find largest 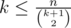such that k|n and that's just binary search on array with factors.I was 100% sure that this will pass.. Really looking forward for solution!

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    root(N) passes pretty easily.

    → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +10 Vote: I do not like it

    you wrote: for(int i=1;i*i<=n;i++)

    i*i=1e10

    overflow, and TLE :D

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Thanks,hopefully Educational round :D

      → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      yes，I get TLE because k*(k+1)/2 is greater than long long.my solution is sqrt(n).But I did't find the error.So I failed the test.What a sad story it is.

      → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    First two solutions works in O(n). In the third one you have integer overflow in factorization, so for big n it is an infinite loop.

    → Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Why is my solution for Problem C not passing.?

My idea is suppose that mid is the gcd of all the numbers then, the smallest form of the numbers is

A = 1*mid, 2*mid, 3*mid, ..., k*mid.

Now consider n-sum(A); This value must be a multiple of mid; simply add this remainder to the last item in A.

We can find mid by binary search.

My solutions always fails on test 14. I think my logic is wrong but why?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Because it isn't a monotonic function so you can't use binary search for it.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      No it is,that array of divisors is sorted,solution works.I got silly overflow because used int in loop.

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it

        He didn't mention that he did binary search over the divisors so I guess he did it over all numbers. Btw, you don't need binary search, you needed to calculate all the divisors so simply see if it fits over all divisors, the complexity is the same.

        → Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 4   Vote: I like it 0 Vote: I do not like it

    I misread your comment. Your solution is the same as mine. Maybe your "mid" value was not selected correctly. Did you check all the divisors of n to choose the optimal mid?

    You have to make sure that n / mid >= k(k+1) / 2

    → Reply
»
8 years ago, # |
  Vote: I like it +41 Vote: I do not like it

Problem G basically.

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +23 Vote: I do not like it

    One segment tree (used twice) is enough.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      i guess i did overkill as i had a normal segtree from [1..K] and a persistent segtree in each leaf node of this segtree.

      → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it +15 Vote: I do not like it

      Can you please explain how?

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
        ← Rev. 2   Vote: I like it +5 Vote: I do not like it

        I just got AC with a normal segtree and an implicit segtree.

        What I did was maintain an implicit segtree over the range [1, N * K], and a normal segtree over the given array, i.e. [1, N].

        The invariant of the implicit segtree is that for every node, if it exists, it will store the correct minimum value of the range it represents. It will also store a lazy value, which if non zero, means that there was an update at some time on the range it represents, with the value of lazy.

        Now when you are updating on the implicit segtree, say the current node completely overlaps with the update interval, then I will mark the lazy value on this node as the current query's value, and free all the nodes in the subtree of this node, since they are not needed anymore.

        When I am querying, if I reach a node that completely overlaps with the query interval, and the node is allocated, I will just return the minimum value at this node (which is correct because of the invariant of the implicit segtree).

        If I reach a node that completely overlaps with the query interval, but hasn't been allocated, I will first see the lazy value of the closest allocated ancestor of the current node which has a non zero lazy value. If their exist an ancestor with a non zero lazy value, I will return that lazy value. If there doesn't exist any such ancestor, I will query over the segtree made over the original array, as this range hasn't been updated in any way.

        It's kind of hard to explain in words, you can try to read the code and see if it helps: Code

        → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
        ← Rev. 3   Vote: I like it +25 Vote: I do not like it

        Let's write down all values of l and r for all queries, sort them and remove duplicates. One can see that a range between two consecutive elements can be treated as a point (because no query splits it) and there're clearly O(q) such points.

        We can build a standard segment tree over this compressed array of query boundaries. Each position should contain a value equal to the smallest element in the given range in the initial array (we can find it using the same segment tree build over the input array. We need to handle "long" ranges carefully: if r - l > n, we can just return the minimum of the entire array). After that, each query is a range assignment/range max in this segment tree.

        → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +12 Vote: I do not like it

    so that's what div 1 people do after solving all the questions...make memes :P

    → Reply
»
8 years ago, # |
  Vote: I like it -8 Vote: I do not like it

Couldn't solve D because of writing while( ++idx && idx < n ) instead of while( ++idx < n )

→ Reply
»
8 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Any idea how to solve F?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +16 Vote: I do not like it

    dp[i] = number of subsequences with gcd i
    dp[i] = 2^c — dp[2i] — dp[3i] — dp[4i] — ..... where c = number of multiples of i.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      Would you explain more details about why and how to use the formula?

      → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      that was easy! feel stupid not being able to solve this one.

      → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    GCD is 1 if and only if GCD isn't multiple of a prime

    So you are looking for |G'(2) n G'(3) n G'(5)....| n is intersection and G(i) means answers where gcd is multiple of i and G'(i) is G negated. Negate this twice and you'll get |G(1)| — |G(2) U G(3) U G(5) ...| use inclusion-exclusion and there you go. G(i) = 2^(frequency of multiples of i) — 1

    → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Is there anyone who may know how to solve problem F?

My solution is O(n log^2 max(a)) but I got TLE.

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

nice problems <3

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by awoo (previous revision, new revision, compare).

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can anyone please explain the solution of problem C?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it
    1. The intended gcd value should divide n.
    2. The minimum possible sum of a sequence of length k with a fixed gcd is equal to gcd + 2 * gcd + ... + k * gcd. Iterate over divisors in decreasing order and try all of them as gcd's. The first sequence sum that is less or equal to n gives you the answer (given you fix the last element if needed).
    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      thank you very much, managed to AC.

      → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Why should intended gcd value divide n?

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        sum of a_i = n Moreover, each a_i can be represented as gcd multiplied by some x_i according to gcd's property. -> sum of gcd * x_i = n ;)

        → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Why does iterating over an array of all divisors get TLE in C? Isn't the max number of divisors quite a small number?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    The maximum number of divisors among all numbers in range [1..10^10] doesn't exceed 2304 :)

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I had a similar upper bound but my solution got TLE. Probably because of cout. :|

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it +3 Vote: I do not like it

        No. I hacked many solutions (yours fails this aswell) with long long overflow) Check something like n = 1, k = 3 500 000 000

        → Reply
        • »
          »
          »
          »
          »
          8 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          So it's actually WA. I had it in my head that k must me < 10^6 but forgot to include it in code :|

          → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In Problem E, I don't understand the line There is no hand such that the absolute difference before this hand was equal to k., can anyone please clarify?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I think it means that the game ends when the absolute difference of number of wins and losses is k.

    → Reply