AmericanPsycho's blog

What are all topics and algorithms about flows?
By AmericanPsycho, history, 8 years ago, In English

All I have read about flows is Edmonds Karp’s Algorithm, which works for maximum flow, but I have seen that there are better algorithms than this one, and there are different problems that maximum flow (like mincost, dinic and others), I would like a list of all the topics and algorithms that are useful for learning network flow!

Thanks in advance!

  • Vote: I like it
  • +8
  • Vote: I do not like it

»
8 years ago, # |
  Vote: I like it -38 Vote: I do not like it

Just google ffs

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +32 Vote: I do not like it

    why do you need to be rude? I don't think it is easy to google all these as the topic is really broad and not CP specific, so it would be nice if there is someone experienced that can summarize it as well.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it -9 Vote: I do not like it

      It is

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it +10 Vote: I do not like it

        well, not everyone is as good at googling and understanding long wikipedia and fancy math notation as you! :)

        → Reply
»
8 years ago, # |
  Vote: I like it +37 Vote: I do not like it

To solve a network maximum flow problem you can use the Edmonds-Karp algorithm. It's a bit long, but it's easy to understand.

However, like you said, there are some variation that make Edmonds-Karp not neccessarily the best option.

I know there are a lot of algorithms that solve the max flow problem, but here is a list of the must used algorithms in competitive programming, and some useful topics:

  • Edmonds-Karp Algorithm (Solves the max-flow in O(VE2))

  • Dinic's Algorithm (Solves the max-flow in O(V2E))

  • Bipartite Matching, a special case of the matching problem, which can be solved applying Edmonds-Karp via DFS.

  • Hopcroft-Karp Algorithm, solves the bipartite matching problem with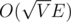 overall complexity

  • Max Flow — Min Cut Theorem

  • Min Cost Max Flow problem, can be solved using an Edmonds Karp variant, replacing the BFS with a fast Bellman-Ford implementation

  • The assignment problem (and Min Weight Bipartite Matching), can be solved using min cost max flow

  • The Hungarian Algorithm, solves the assignment problem with O(n3) complexity

  • Push-Relabel Algorithm

  • König's Theorem

  • Dilworth's Theorem

The last two theorems allows us to solve the Minimum Vertex Cover and Maximum Independent Set problems in bipartite graphs using flow algorithms

One of the most important things about these kind of problems is to find that it is indeed a network flow problem. That's why these topics require a lot of practice.

Personally, I find very hard to understand some algorithms like the Hungarian Method, so it is important to prepare a good library with these implementations. This way we avoid the struggle during contests!

Hope you find this list useful :)

→ Reply
»
8 years ago, # |
← Rev. 3   Vote: I like it +20 Vote: I do not like it

I think the topics provided by snacache is enough comprehensive. I'm going to share some links which helped me while learning network flow.

  1. Go through the 4 max flow tutorials from Topcoder tutorials index

  2. Explanation of complexity of Edmonds-Karp (I personally had a tough time understanding the reasoning behind the complexity until I saw this answer. )

  3. Links for understanding Dinic:

  1. For mincost maxflow go through the 3 mincost maxflow tutorials given in the first link for topcoder tutorials

  2. Mincost Maxflow with SPFA (Shortest Path Faster Algorithm) achieves a better average case complexity than mincost maxflow with Bellman Ford. Learn SPFA from here

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    mind sharing insight like when to use dinic and when to use edmonds? Or is it solely on how dense the graph is?

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
      ← Rev. 2   Vote: I like it +7 Vote: I do not like it

      I actually always use Dinic. Dinic's worst case complexity ( O( V^2 * E )) is better than that of Edmond Karp ( O( V * E^2 ) ). And I haven't heard that Edmond Karp works better in any special graph than Dinic.

      → Reply
»
8 years ago, # |
  Vote: I like it +6 Vote: I do not like it

I see others have described the algorithms and problems, I'd just add the link to an efficient implementation of Diniz's algorithm here. The page is in Russian (the English version of the page doesn't have Diniz's algorithm yet), Google Translate is your friend. Page also includes efficient implementations of other algorithms in C++.

→ Reply
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Atcoder is having a lot of flow problems in ABCs these days. Can someone please share the list of flow problems if one has compiled.

→ Reply