→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
20:02:02
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
20:02:02
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 22.11.2024 21:32:59 (i1).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











в 15:10.
Ни у кого нет проблем с регистрацией и коннектом?
есть
В Kawigi написал решение, отправил его, но почему то он отправил предыдущий run но локально сохранил текущий. Почему так произошло, и как с этим бороться? P.S в первый раз его использовал
сраная 555, понятно что делать, ну с*ка, пока напишешь эти 100500 динамик
100500=1? Да и та — предподсчитать C(n,k).
можешь рассказать это решение?
Предподсчитаем все цешки до 3100на3100. Далее переберем двумя циклами сколько столько строк инвертировали нечетное число раз (пусть их a, всего строк n) и сколько столбцов инвертировали нечетное число раз (пусть их b, всего строк m). Тогда несложно увидеть, что число единичек в таблице ровно a*(m-b)+b*(n-a). Если это число совпало с S, а числа Rcount-a и Ccount-b четные неотрицательные, то к ответу надо добавить C(n,a)*C(n+(Rcount-a)/2-1,(Rcount-a)/2)*C(m,b)*C(m+(Ccount-b)/2-1,(Ccount-b)/2). Разбираем что это такое — C(n,a) — это мы выбрали какие строки будут "нечетными", на их обслуживание надо сразу же потратить a преобразований над строками. Теперь у нас осталось Rcount-a преобразований над строками и они идут парами, т.к. теперь уже все строки должны быть инвертированы четное число раз. Причем эти пары можно раскидывать как угодно. Перешли к стандартной задаче разбить число (Rcount-a)/2 на n целых неотрицательных слагаемых. Это число способов равно в точности C(n+(Rcount-a)/2-1,(Rcount-a)/2). Остальные два сомножителя — аналогичные для столбцов. Вот и все.
спасибо за объяснение, но я уже сам решил только цшками... однако, не самая лучшая идея, писать сразу, что пришло в голову на контесте
расскажыте свою идею неС-шками
честно говоря это треш, но все же тоже зашло: понятно что нужно разбить rcount на h слагаемых и ccount на w, причем, если среди h слагаемых ровно i четных, а среди w слагаемых j четных, то единиц будет i(w - j) + j(h - i)
научимся считать следуещее: количество разбиений числа n на m слагаемых, что среди слагаемх ровно p четных (понятно, остальные m - p нечетные)
будем делать это так: посчитаем динамику even[x][y] — количество разбиений числа x на у слагаемых, что все y слаегаемых четные, а так же динамику odd[x][y] — количество разбиений числа x на у слагаемых, что все y слаегаемых нечетные, понятно, как считать эту динамику: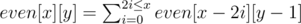
odd[x][y] считается аналогично
заведем теперь динамику f[p] — количество способов разбить n на m слагаемых, что среди слагаемх ровно p четных
и действительно, это количество разбиений в котором $p$ четных чисел, которые в сумме дают i, а остальная сумма набирается нечетными слагаемыми. Cmp берется из того, что мы на какие-то p мест поставим четные числа, на остальные m - p мест нечетные
теперь мы имеем два массива frow и fcolumn, теперь надо пробежать по (i, j) — количество четных элементов в строке и столбце (в разбиении строки и столбца на слагаемые) если i(m - j) + j(n - i) = s прибавим к ответу frow[i]·fcolumn[j]
PS. от дурной головы, рукам покоя нет, вот это все писал
по крайней мере у вас есть своя и правильная идея..не то, что у других — отсутствие каких либо идей ;)
Красиво.
Эм? Там все через цшки считается
ну это таргеты может через цшки все там считают, а в моей комнате много решений (подавляющее большинство), как и у меня, это >=2 динамик
Ну так тогда может не задача виновата?
Вон в харде вообще 2 принципиально разных решения в зависимости от "ширины программы" — и я не жалуюсь
В свете результатов систестов хотелось бы узнать как решался хард.
А можно тогда поподробнее пожалуйста, про второй тип решения ради интереса?
Я придумал но не успел накодить, что сделав backtracking перебрав конечные позиции и получив строку из '0', '1' и '?' (что угодно), если их меньше половины (потому что диапазон движения бегунка больше половины), то катит inclusive-exclusive, а если их больше половины, то диапазон движения меньше половины, и следовательно вопросительных знаков меньше половины и катит перебор с set'ом.
Ну да, либо включение-исключение, либо полное построение, это и есть те 2 принципиально разных решения
И насчет бактракинга я не понял — мы просто с каждой позиции берем момент, когда последний раз строка могла быть валидной
А как быстро включение исключение считать?
Да вроде бы должно проходить и 2^18 * 18 * 36. На всякий можно было попробовать чуть уменьшить границу для включений.
Проходит и так. У меня под завязочку как раз — 1.3 с одной стороны и 1.6 с другой. То есть было бы хотя бы 37 ограничение — пришлось бы оптимизить
А, ну и границу для включений у меня не получилось бы уменьшить еще и из-за МЛ
А откуда число 18 взялось?
Потому что если различных масок > 18, то это значит, что число вопросительных знаков в каждой маске не больше чем 18, и вместо включений можно делать перебор с сетом.
Добавил тупой перебор если масок много и прошло в практисе. Жаль мог на СРМе сдать первый "настоящий" хард
Под backtracking'ом я имел ввиду, что получаем маску для фиксированной конечной позиции, откатываясь назад: '<' и '>' инверсируются, а цифра либо crash'ит текущую позицию, если не совпадает, либо превращает текущий символ в вопросительный знак, если совпадает. Кажется термин backtracking тут что-то был не к месту...
могу сказать про свою комнату, все, кто решали, решали с помощью C-шек.
Моё решение по 1000-ке (не успел найти баг но на практисе сдал)
Найдем множество масок M такое что : начальное X хорошее <=> для какой-то маски M из множества X & not M == goal & not M
Для каждой стартовой позиции выполняем действия, помня маску изменений. Если в какой-то момент обрабатывая goal мы бы получили опять же goal, добавляем эту маску в множество. Дополним множество так, чтобы для любых масок A, B из него, A&B тоже было в нём.
Утверждение: таких масок мало, т.к. они все подмаски какой-то циклической сдвинутой хрени.
Остаётся просчитать включение/исключение, рассмотрим какой вклад вносит отдельная маска в ответ: это 2^(кол-во единичек) за вычетом вкладов всех подмасок которые есть в нашем множестве. Сумма вкладов и есть ответ.