Суть моего решения: Храню текущую позицию и ищу от неё ближайшую диагональ(при условии, что не надо идти назад). Складываю кол-во пройденных диагоналей. Ответом будет максимальный путь минус экономия от диагоналей, т.е
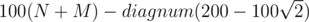
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 4 | atcoder_official | 161 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
Суть моего решения: Храню текущую позицию и ищу от неё ближайшую диагональ(при условии, что не надо идти назад). Складываю кол-во пройденных диагоналей. Ответом будет максимальный путь минус экономия от диагоналей, т.е
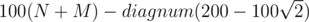
| Название |
|---|



Ближайшая диагональ может не быть глобально оптимальным выбором. Возможно, после ближайшей все остальные диагонали остаются "позади", а если бы выбрал какую-нибудь другую, имел бы шанс срезать ещё на следующих.
а какой выбор тогда будет глобальным?
Невозможно сказать заранее. Или нужно рассмотреть все возможности (с помощью динамического программирования), или же рассматривать задачу с точки зрения теории графов (получится просто задача на кратчайший путь).
хм. а что тогда принимать за вершины графа?
Можно тупо взять (N+1)*(M+1) вершин — все точки в прямоугольнике [0, N] x [0, M]. Можно видимо и 2+2*K вершинами обойтись — начальная и конечная точки + концы диагоналей.
Динамикой надо решать, a[i][j] — минимальное расстояние до клетки (i,j).
Т.к. полная матрица 1000 x 1000 не лезет в MLE, надо хранить два столбца и чередовать их.
Ещё один способ не получить Memory Limit — завести матрицу не int, а short
Я проверял такой способ только в C++
разобрался сделал матрицу с вершинами- точками в системе координат(только хранил их в short). В матрице хранил кол-во диагоналей при минимальном пути к каждой точке. Потом по формуле, которую я написал, вычислял