Description: A set of points P and a set of target points M in 2D space are given,. For each point M[i] in M, find the minimum angle at M[i] such that all the points P[i] in P are contained within this angle. If the angle is not less than 180 degrees, then you just have to output “TOO WIDE”.
Constraints: 1<= N,Q <=100000
My approach: First I find the convex hull and then check if the query point is in the convex hull. If it is in the polygon then the answer will be "TOO WIDE" . If not then I do as follows:
Find the centroid of the polygon and then find the angle of the vector "centroid to Pi" with x axis, where Pi represent points of the convex polygon.
Eg. if centroid =(0,0) and Pi=(1,1) is one of the points of polygon then the angle of the centroid to Pi vector is 45 degree. If Pi=(-1,-1) then the angle = 225 degree.
Then sort the points with respect to their angle. When I got a query point M then I again calculate the angle of the vector "centroid to query point M". Now I cut the polygon into two half with the line passes through the centroid and M. Then for each half I do ternary search and finally find the point X and Y as shown in the figure.
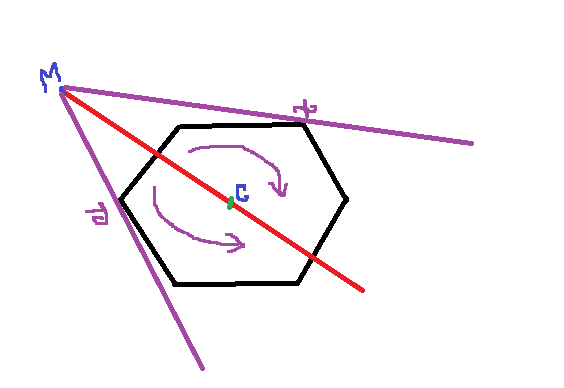
[In figure , C=centroid , M=query point and black lines represent the convex polygon]
Thus I find the angle (X,M,Y). But my approach is seemed to be incorrect and I cannot figure out what I do wrong here. Was my approach correct? Is there any other approach to solve this problem?
-Thanks in advance.











Just an idea to solve the problem offline (I'm not sure if it works, but it seems ok). I'll consider the points which should be in the angle to be only the points on the convex hull. As you noticed, for each query point we need to find the "leftmost" and "rightmost" point in the polygon and the angle between these two vectors is the answer. Now, let's sort the query points in order of their angle and the center of the polygon. For the first query, simply bruteforce the solution(I believe you'd do it). Then, if we move clockwise in the sorted query points, you can notice that the two points from the polygon we are looking for will also "move" clockwise. This gives us the idea to do something similar to the "sliding window" technique. And in fact, due to the sorting, it seems to me that no point will get in our "window" twice, so this search is linear. The last part is where I'm not sure, but if someone confirms this, I believe this algo is OK and will fit in the constraints.
I also though about this, but it is not right. You can see this in picture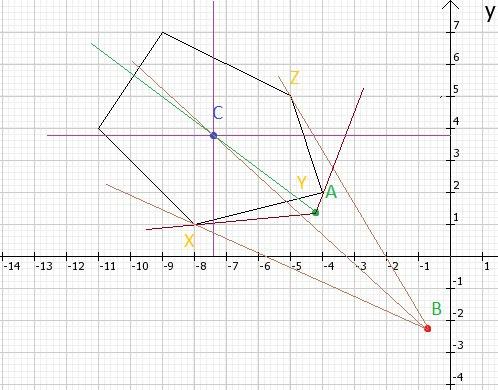 .
.
Point A is to the left of B in sorted array, but rightmost point shifted back.