I have an array a of values +1 and -1 in random order, and a separate array s which is initialised with 0 in every position. I run through the array from left to right. At every index i, I add the value of a[i] across s[0], s[1], ... , s[i-1], s[i]. And at every index i, after doing the previous operation, I want to return the rightmost index in the range [0, i] with value 0. If no such index exists, I'll return some invalid number like -1.
The adding operation can be done using a Fenwick tree. But I have no clue to find the rightmost index in logarithmic complexity. I'm trying to do the entire process in O(n) or O(nlogn) complexity. Any idea would be much appreciated, thanks!











Let's start by observing that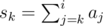 after adding element ai. Then we can see that s1 = s0 - a0, s2 = s0 - (a0 + a1), and so on. (
after adding element ai. Then we can see that s1 = s0 - a0, s2 = s0 - (a0 + a1), and so on. (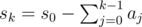 ). If sk = 0, then
). If sk = 0, then  . We can store every element of the prefix sum array (let's call it c) of a in a
. We can store every element of the prefix sum array (let's call it c) of a in a
map<int, vector<int>> m, whose keys will be the values of c which will map to the indices in which they occur. (i.e.m[c[k]]will hold all indices j, such that ck = cj). Updating s0 in constant time should be obvious. After every update, we will checkm[s[0]], and find the rightmost index j such that j ≤ i using binary search.Edit: We can also use a
map<int, int>, which we can use to store the rightmost index at which we have encountered s_0 before.Oh, sorry if I wasn't clear enough. For the input
1 -1 -1 1 -1, my output would be (zero indexed)-1 0 -1 2 3while your code would give-1 -1 -1 1 2.Fixed (I think). Try the other approach if it still doesn't work.
I don't think you need any data structure.
Just observe that for at any i, s[j] = 0 if a[0] + ... + a[j] = a[0] + ... + a[i]. So at every iteration, keep track of the total sum, and find j such that a[0] + ... + a[j] = total sum. And this can be done with partial sum in O(1) for each iteration.
You can do this in O(NlogN) by using Segment Tree, but I'm pretty sure an O(N) solution can be found by making some observations and math.