TopCoder Open 2017 Round 2C, together with a parallel round, starts in a little less than an hour. Let's discuss the problems here after the contest.
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | jiangly | 3846 |
| 2 | tourist | 3799 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3590 |
| 6 | Ormlis | 3533 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3463 |
| 9 | ecnerwala | 3451 |
| 9 | Um_nik | 3451 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 165 |
| 2 | -is-this-fft- | 161 |
| 3 | Qingyu | 160 |
| 4 | Dominater069 | 158 |
| 5 | atcoder_official | 157 |
| 6 | adamant | 154 |
| 7 | Um_nik | 151 |
| 8 | djm03178 | 150 |
| 9 | luogu_official | 149 |
| 10 | awoo | 147 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Mar/11/2025 09:22:04 (j1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










Is it open for everyone, or we need to qualify through the previous rounds?
You need to have qualified from the Round 1.
Hi, I'm the author of the hard problem.
It's obvious to solve it in polynomial time using dynamic programming, with f[i][j] denoting the minimal sum we can get by splitting the prefix of length i to j parts.
The key observation is that for any i, j, f[i][j] - j < 26. Therefore, let g[i][j](j < 26) be the minimal k such that f[i][k] - k ≤ j. It is easy to do DP on g, solving the task in O(262 × n) time.
How do you compute it in
O(26n)time? A solution withO(26^2 * n)time complexity passes anyway, but how to get rid of another alphabet size multiplier?Sorry, I wrote the wrong complexity. Fixed now.
I made the same observation in the first 5 minutes and kept trying to find out how to compute g till the very end. If G(i) were undecreasing, it'd work, but it is not. For example string abc has g: 2 1 0
I dunno why you need g to be undecreasing. Obviously, g is non-increasing, so if g is undecreasing, all elements would be the same.
Ohh now I see. I needed it to have some sort of monotony. I'm sad that I wasted my first chance to solve the hard. The problem is absolutely stunning and natural. Congrats on creating it. Hopefully, next time I'll be able to take advantage of a good observation.
Is min cost max flow the right approach for the 500 points problem?
Yes, angel wins if cheapest flow of size D+1 is of cost <=A, on a complete graph where edge's cost is 1 iff it doesn't exist in initial graph and 0 otherwise. Demon wins if D>=n-1.
New achievement: Write a code that will give you a spot in third round, but don't submit it.
I did second problem, but I didn't know that A>=2 and spent half of a contest wondering what if A=1 ._. ... In the meantime I wrote actual solution to my problem without A=1. It passed in practice room.
@authors Yeah, it would be great thing to put constraints like A, D ≥ 2 in the statement next time.
I also work hard in handling the case A=1...
By the way, A = 1 is solvable.
Let's check if Demon has a winning strategy (nothing special happens for Angel). Let's call edges in the original graph "black", and Demon's edges "red". Demon wants to split the vertex set into three parts S, T, U, and color at most D edges red, such that
So, we want to find a partition S, T, U that minimizes (the number of black edges between U and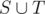 ) + |S| × |T|. Obviously, |S| or |T| should be 1, so this is (the number of black edges between U and
) + |S| × |T|. Obviously, |S| or |T| should be 1, so this is (the number of black edges between U and 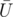 ) + N - |U| - 1. It's not hard to reduce this to a mincut problem.
) + N - |U| - 1. It's not hard to reduce this to a mincut problem.
I believe Demon could win if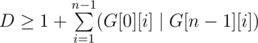 in case A=1
in case A=1
I believe following graph is a counter example.
You are right
how to solve 250?
Consider the foxes ordered in increasing order (by weight). Notice that swapping any two adjacent elements A(i) and A(i + 1) (where A(i) < A(i + 1)) can increase the answer by at most 1. So, keep doing the following:
I wrote an optimised exhaustive search. At each step the minimum and maximum result was calculated with remaining foxes, sorting foxes in decreasing and increasing order, respectively. If k was between the minimum and maximum, then continue search in this direction, otherwise go back. When minimum is equal to the maximum we found the answer. I had little confidence that would pass the system tests, but it did.
My 250 problem solution got successfully challenged. Is there any way to get testcase? (new to topcoder)
I used bubble sort to solve it.
If anybody has some time to spend here's my code: https://paste.ubuntu.com/25147848/ (I know this is shit code)
Link : https://community.topcoder.com/stat?c=problem_solution&rm=330384&rd=16951&pm=14651&cr=23303116
In all three TCO2 rounds I solved hard, but failed medium. What is wrong with me? :)
Samples for 500 are super weak, my garbage code passed them (it completely ignores edges non-adjacent to 0 or n - 1).
Also, I think 2C should've been kind of easier, since there are at least 80 top people who can't participate. This was way too... hacky.
I can discuss one problem that TC has. I've finished hard 2 minutes after the end of the contest, it was correct and would give me advance to next rounds. I am writing TC contests in webarena, because I don't know how to hack on normal arena and only possibility to learn is during the contest, and during the contest there's no time to learn how to use a plaform. Because of TC's input limit (more problems, yay!) there was an input generator in hard problem, and normal arena was showing it like this:
So yea, ok, normal code, I can translate it into c++ fast. But webarena was showing it like this:
So for several minutes I was wondering what is this ">=" shit, is it some magic python function, or is one of parameters named "gt" and it's some reference, I was also searching for a way to ask a question about it, but I didn't find any option to do that...
Did I already told that I think about codeforces vs topcoder?
Nope. You can hack in practice rooms. Maybe you can submit crap and try to hack yourself to learn, but I'm sure there's plenty to hack even if not.
Last time I remember, the web arena had a lot of bugs. Like randomly vanishing codes.
> is HTML for > (greater than), < is < (less than) to avoid parsing as HTML tags. Trying to parse one thing in many different ways is absolute cancer, you'll get stuff like having to write 4 backslashes in a row in order to render something invisible.
I still have no idea how to build larger tests in the arena. I've tried a couple of ways and still don't know. Could you tell us, for example, how you can build a 50-element array?
Write a generator, run it locally, copy the result and click
{}. The exact syntax for an array is{a[0],a[1],..,a[n-1]}.Needs a lot of trial and error to find out, though.
My plugin has this issue as well and I found it before the contest, but I thought it was just because my plugin sucked, and didn't pay much attention. This may be the reason why administrators didn't find it either.
If I type '<', it will fail because '<' is special in HTML. That's why I used >.
Sorry for wasting your time.
The applet shows a poor stack-trace sometimes for Python programs. It points to some line in their backend's Python wrapper. I understand that the error message can be used to trace back and figure out where my code screwed up, but maybe a cleaner solution could be possible to point the origin of the error in my code.
BTW, if you use arena applet, you can contact admins by using the chat box at the bottom. By clicking the ">>" button on the left side you can set your receiver as admins.
Random finding: If you're using a Mac and if
Cmd+C/Cmd+Vdoesn't work for copy/paste on the Topcoder Applet, usectrl+C/ctrl+V.A and D will be between 2 and n*(n-1)/2, inclusive.
I didn't notice "2", and wasted about 60 minutes.......
My 500 failed, but passed after fixing an implementation bug.
This solution uses maxflow only. Can you prove it or find a counterexample?
We're trying to maximize maxflow after adding A edges. Evidently one additional edge can increase maxflow at most by 1. So, I test each of edges 0~i and (n-1) to see whether adding it makes the maxflow bigger. If so, I maintain the edge in the graph. Let's call the number of added edges as E.
For all other cases I assume 2 additional edges can increase maxflow by 1.
So, Angel wins only if maxflow(graph) + min(E, A) + (A — min(E, A)) / 2 > D.
The way I thought is similar and shows why this works.
We're trying to maximize maxflow after adding A edges. The edge (0, n - 1) is easy. If the path 0, i, n - 1 exists for any i, then we can send flow through that path — if, after adding edges, one edge from that path was used in the flow and the other wasn't, then we can redirect the flow; if both were used in different paths from 0 to n - 1, we can switch parts of those paths at vertex i.
Now, let's find some paths to complete the maxflow. As long as w.l.o.g. the degree of 0 is less than of n - 1, we can find an edge (i, n - 1) that isn't in one of those paths, meaning (0, i) didn't exist and we can add it, increasing the maxflow by 1.
As soon as this isn't possible, the maxflow can be increased by 1 only at cost ≥ 2 (since the degrees of 0 and n - 1 are equal to the current maxflow). Cost 2 is also sufficient since we can add edges (0, i), (i, n - 1) if they didn't exist or (0, j), (i, n - 1) if there was a path 0, i..j, n - 1.