For a = 1 and b = n the task is to find the point (A, B) with maximal projection to the direction (x, y). Now it is very similar to "how many points under the line" queries.

Some discussion about it.

UPD: ok, after yeputons's comment mine is useless

Note that erase is not equivalent to setting A_i and B_i to  - ∞, because one can then choose negative x and y and get  + ∞ as an answer. On the other hand, if you have removals only and it's offline, you can reverse the order of operations and now you have additions and queries only. And additions can be replaced with "enable" queries.

If we treat A_i and B_i as vectors on the Euclidean plane, each query basically asks us to find a vector V_i among V_a, V_a + 1, ..., V_b such that V × V_i → max (where V = (a, b)). Let's get rid of range queries for a moment and assume that a = 1 and b = n for all queries. Now we simply have a set of vectors and we want to maximize dot product with an arbitrary vector V. What is dot product? It's basically some kind of "how far in this direction this point lies" measure. Or, in some other sense, it's a directed distance from some line. Anyway, that problem is classical and it can be solved by computing convex hull of V_i and then using some special kind of binary search by angle to find the answer.

That is, if a = 1 and b = n, we can answer queries online in after preprocessing. If we add segment tree here, we get preprocessing (that possibly can be made even after if we merge convex hulls instead of re-building them) and 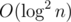per request.

To support "adding" points we only have to learn how to add a point to a convex hull fast enough, and then we will just add a point to convex hulls. Now that's another classical problem which can be solved using some self-balanced tree (e.g. treap), binary search in that tree and finding tangents to a convex polygon using that binary search and ternary search. I believe that it can be done in in one convex hull, resulting in 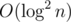time per original query.