awoo's blog

Educational Codeforces Round 26 Editorial
By awoo, history, 7 years ago, translation, In English
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
  • Vote: I like it
  • +33
  • Vote: I do not like it

Comments Comments (38)
| Write comment?
»
7 years ago, # |
  Vote: I like it +54 Vote: I do not like it

contribution of a0[i] in ar[n] is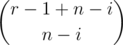
Using this and binary search on answer , you can solve this in NlogK

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 3   Vote: I like it 0 Vote: I do not like it

    Just hijacking the thread -- I think I have seen the steps of deriving this equation in a HackerRank problem classified under mathematics, but I couldn't find it. In case if someone finds that proof please do me a favor and put the link below.

    Edit: Speak of the devil, found it. https://www.hackerrank.com/challenges/divisor-exploration-3/editorial .... forget it, it's not the same thing.

    → Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 3   Vote: I like it 0 Vote: I do not like it

    rajat1603 Can you explain how(about the contribution)?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      contribution of something in ar[c] is sum of its contribution in ar[c - 1] and ar - 1[c] , this formula looks like the formula for number of paths between 2 points in a 2d grid for which the formula is well-known.

      → Reply
  • »
    »
    11 months ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    same

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Is there a name for the type of function in G? It's some combination of Sigmoid and ReLU, but I couldn't find it's name...

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    It has a jumps so it is quite useless and can't have own name.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Oh, I meant the version without jumps. Is there name for that?

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        f(x) = max(l, min(h, x)) is called clamping and C++ has std::clamp to do that. I don't know about a specific name, but the function is basically clamp multiplied by a and then added by an offset of b.

        → Reply
»
7 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Can anyone help me in understanding the rationale behind choosing the way the dp is being done? Why the 3D approach? How was the logic arrived at? Is there another, more intuitive way? Thanks!

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +7 Vote: I do not like it

    When I look at this problem I think: "Okay, the answer depends on 4 parameters: how many numbers we processed, how many chosen to subset, what power of 2 divide subset, what power of 5 divide subset". Then I chose 3 of the parameters as DP state, and one (largest) as DP value. Is it intuitive enough?

    → Reply
»
7 years ago, # |
← Rev. 7   Vote: I like it +1 Vote: I do not like it

Could somebody explain the way we store all possible summary powers of 5 in dp array? There can be i * log5(1018) variants, and if we will iterate through them all n2 times (including non-existing), it will waste too much memory ..

I tried to use map to exclude non-existing variants, but n3 * log(n * log5(1018)) got TL: http://codeforces.net/contest/837/submission/29189656

Thanks in advance :)

UPD. Finally got it. We do not need to store current position, only 2 last lays needed (dp[2][200][200 * log5(1018)])

→ Reply
»
7 years ago, # |
  Vote: I like it +10 Vote: I do not like it

My lame F solution that passes:

n > 3 is sufficient to pass the naive approach (after zero prefix deletion). So we should handle n==2 and n==3. For n==2 we can write linear O(1) equation on k, and for n==3 there is quadratic equation on k which can be solved in O(1) or O(log 10^18) using binsearch.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    How did you figure out that a brute force solution will pass whenever N>3?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Just try the worst case: 1 0 0 0... and 10^18

      → Reply
»
7 years ago, # |
  Vote: I like it +16 Vote: I do not like it

On Problem G, I set up four President Tree and the Time Limit seems too tight for me 29192449, maybe I will be hacked sooner or later :)

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it +14 Vote: I do not like it

Simpler solution to Problem E. Without prime factorization. Let d = gcd(a, b); It can be proved that f(a,b) = f(a/d, b/d); if a is prime, then answer is (b % a + b/a); Then the result can be recursively computed. My solution

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Please explain how do you prove the above fact?? I am simply unable to come to it :(

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      It comes from the fact mentioned in the editorial: "when we subtract gcd(x, y) from y, new gcd(x, y) will be divisible by old gcd(x, y). And, of course, x is always divisible by gcd(x, y)." Because of this we always subtract k*gcd(x,y), so we can just divide by k.

      → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

For Problem F - In fact, you can brute force the prefix sums if the array is of size at least 4. In case of size 2 it's super simple. And lastly, in case of size 3 it can be solved mathematically.

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Regarding problem D, does this sentence: "the first dimension should be stored in two layers and recalced on the fly" mean that :

for every position i you only need the result of i-1 so no need to store the results corresponding to positions earlier than i-1 ?

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Anyone can help me to find what's wrong with my solution for problem D? http://codeforces.net/contest/837/submission/29282743

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    you are not checking this case number of power of fives equal to zero. so for 5's 2's 64 0 6 32 0 5 16 0 4 8 0 3 3125 5 0 start your loop for number of power of fives from 0.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      ah, thanks for helping. it got AC now.

      → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

can anyone elaborate this line?

Let dp[i][j][l] be the maximum amount of twos we can collect by checking first i numbers, taking j of them with total power of five equal to l. It is usually called "the knapsack problem".

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    For dp[i][j][l] = n,

    • n is the greatest integer that satisfies 2^n | (the product of the numbers in the selected subset)

    • l is the greatest integer that satisfies 5^l | (the product of the numbers in the selected subset)

    • j is the number of numbers selected from the set (or the size of the subset selected)

    • i is the number of numbers considered

    eg. If dp[3][2][2] = 1, (looking at the first 3 numbers given, selecting exactly two such that 5^2 is the greatest power of 5 that divides the product), 2^1 is the greatest power of 2 that divides the product.

    → Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Task E

Can anybody proove that k in new gcd will be PRIME (that there is no better non-prime k)?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    For any number n=p1*p2*p3.. if the inflexion point(where the gcd changes) is divisible by n then it will be divisible by p1,p2..pn but the converse isn't true.

    → Reply
»
5 years ago, # |
  Vote: I like it 0 Vote: I do not like it

F has a much simpler solution using contribution technique i believe.

→ Reply
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How to solve problem D using top-down approach?

→ Reply
»
3 years ago, # |
  Vote: I like it +1 Vote: I do not like it

How to solve D using recursive dp? Is it possible? I wrote the recursive function to compute the number of twos but it is very confusing how to extract the solution out of it.

→ Reply