Hi! I need some ideas for the following problem.
Given an initial array of zeros and target array, and operation of adding 1 to range [l, r]. Find the minimum number of steps to reach the target array.
I am looking for a solution which is better than O(n^2).
Thanks!











Hi. Is there a link to the problem?
Unfortunately not. This is some interview question and I couldn't find a similar problem anywhere.
You need segment tree with (minimum, position) as values and recursive greedy solution, which get the range, find minimum on it, add (it's value minus already added) to the answer, and split recursion to the left and to the right of min element.
Oh yes! This should work. Thank you!
Isn't it just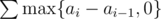 ?
?
Can you please explain why is this correct?
basically for each i, you just need to check the left neighbour's value. If it's greater than the one on the left, you need to add the difference between it, else you don't have to add anything. Though i think the equation is only correct if you set a[-1]=0.
I do see that with this amount of operation, we can have the target array but I do not see why is this value minimum. :/
it's like an induction.
so suppose this is true for n =k(i will leave the trivial base case to you), so for k+1,
we know that the minimum for getting to the first k is the sum from 0 to k (max {a[i]-a[i-1], 0}), and we need to get the k+1th element to a[k+1], and we know that if a[k+1] < a[k], then the answer is sum from 0 to k (max {a[i]-a[i-1], 0}) + 0, which is sum from 0 to k+1 (max {a[i]-a[i-1], 0}), else if a[k+1]>=a[k], then the minimum operation to get the k+1th element to a[k+1] is a[k+1]-a[k], so the answer is a[k+1]-a[k] + sum from 0 to k (max {a[i]-a[i-1], 0}), which is also sum from 0 to k+1 (max {a[i]-a[i-1], 0}). and we are done.