AtCoder Grand Contest 019

→ Обратите внимание

До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
24:41:30
Зарегистрироваться »

*есть доп. регистрация

→ Лидеры (рейтинг)

№	Пользователь	Рейтинг
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

Страны | Города | Организации

Всё →

→ Лидеры (вклад)

№	Пользователь	Вклад
1	cry	167
2	Um_nik	163
3	maomao90	162
3	atcoder_official	162
5	adamant	159
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
9	Dominater069	153
9	nor	153

Всё →

→ Найти пользователя

→ Прямой эфир

Детальнее →

Блог пользователя tourist

AtCoder Grand Contest 019

Автор tourist, история, 7 лет назад, По-английски

AtCoder Grand Contest 019 will be held on Saturday (time). The writer is tourist.

Contest Link

Contest Announcement

The point values will be 300 — 500 — 900 — 1000 — 1700 (1200) — 2000 (1500). Note that the contest duration is unusual (150 minutes).

Let's discuss problems after the contest.

atcoder, agc, agc019

+569

tourist
7 лет назад
41

Комментарии (39)

Показать архивные | Написать комментарий?

Siriuslight

7 лет назад, # |

+33

It is very pleasing as well as fearing to see you as a contest writer tourist.

→ Ответить

ania

7 лет назад, # |

+197

Yesterday I had to cancel my weekend plans and got upset by that. Now I'm not that upset anymore.

→ Ответить

E869120

7 лет назад, # |

+211

tourist round? Oh Yeah!

→ Ответить

-emli-

7 лет назад, # ^ |

+47

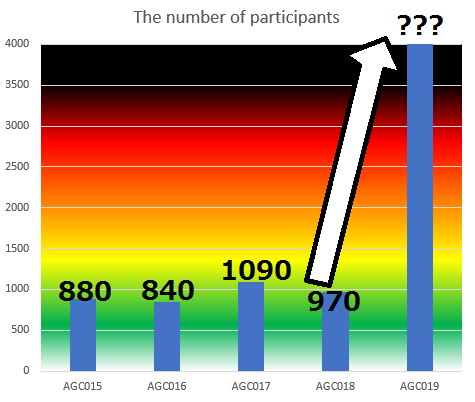
~ 1432 users

→ Ответить

Ashishgup

7 лет назад, # |

+338

Special mention when tourist is the problem setter:

→ Ответить

RailtonT

7 лет назад, # |

+31

I hope to get well in this contest, this wink has to mean something..

→ Ответить

P___

7 лет назад, # |

-14

Looks like the whole world is waiting for this contest -> I hope that servers will handle such a huge number of participants.

→ Ответить

madn

7 лет назад, # |

+21

Did anyone else get WA in last 4 tests in C?

→ Ответить

chemthan

7 лет назад, # ^ |

← Rev. 2 →

+10

Case like that:

0 0 3 1

1 0

2 1

→ Ответить

madn

7 лет назад, # ^ |

I think i considered that, so what's correct output?

→ Ответить

Danlark

7 лет назад, # ^ |

-10

402.831853071795862

→ Ответить

madn

7 лет назад, # ^ |

And how can we achieve this?

→ Ответить

Danlark

7 лет назад, # ^ |

+10

Sorry, my mistake 407.123889803846897

→ Ответить

madn

7 лет назад, # ^ |

I have the same, so i've missed something else

→ Ответить

Neil

7 лет назад, # ^ |

The last 4 cases were similar but with x & y swapped. Try this

0 0 1 3

0 1

1 2

→ Ответить

CMaster

7 лет назад, # |

Any hints for C?

→ Ответить

rng_58

7 лет назад, # ^ |

+79

x₁ = x₂ and y₁ = y₂ are not the only special cases.

→ Ответить

nima10khodaveisi

7 лет назад, # |

how to solve B ? :)

→ Ответить

mbrc

7 лет назад, # ^ |

+24

Consider all contiguous regions.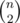 $\text{[math]}$ of them. Now a [l... r] is superfluous if a[l] = a[r] as [l + 1... r - 1] is already checked. Subtract these from that.

→ Ответить

nima10khodaveisi

7 лет назад, # ^ |

okay thanks :)

I get it :D

→ Ответить

-Morass-

7 лет назад, # ^ |

+29

Good day to you,

well a good hint is, that as long as "borders" of reversed substring are equal, then the string after reverse will be same as if it was reversed without borders.

Also note that if this wouldn't happen, then |s|*(|s|+1)/2 (+1) possible solutions could apprear.

Hope it helped a little bit.

Good Luck & Have Nice Day ^_^

→ Ответить

nima10khodaveisi

7 лет назад, # ^ |

oh okay :P

I was so stupid :)

thank you :)))

→ Ответить

tubo28

7 лет назад, # |

← Rev. 2 →

+20

Solution for B is so simple but too difficult to come up with. ;(
How did you come up with it?

→ Ответить

Len

7 лет назад, # ^ |

← Rev. 2 →

+10

It's obvious that if substring is palindrome reversing it won't change anything. And I noticed if s[l] = s[r], then reversing it will be same as reversing [l + 1, r — 1], so you need to substract such pairs.

→ Ответить

ania

7 лет назад, # ^ |

+156

The hard way:

"prove" that any palindrome is bad and any non-palindrome is good (and unique)
code a solution using Manacher's algorithm
fail last sample (answer: 54)
print all strings my solution generates
find out why some are the same
look for a way to find pairs of same letters in same distance from given pivot (yay for overcomplicating)
give up, switch problem
return to it, start from scratch but with a correct condition this time
finally solve it.

→ Ответить

mshcherba

7 лет назад, # ^ |

+23

My first three steps were the same as yours :)

→ Ответить

mbrc

7 лет назад, # ^ |

← Rev. 2 →

+55

Then atleast someone suffered like me. My steps:

Look at points : 500 => Easy.
Look at problem : WTF, how to solve?
Think for some time, figure out swapping palindromes is invalid.
Look at "abracadabra" : HTF is answer 44? How can 11 be bad?
Look at standings : People solving trivially in 8 — 10 minutes.
Start discarding Manacher. What is trivial and seems correct?
No idea, write brute force Python code, print all invalids.
Endpoints equal means invalid, scold yourself for being dumb.
Believe in God, and that your observation is the sufficient condition.
Code.

→ Ответить

nima10khodaveisi

7 лет назад, # ^ |

-25

and these are my steps :D :

1.read problem !

2.WTF :D

3.after about 10 min think , I guess that it need some algorithm that I don't know !

4.close contest page and go to my bed and sleep :))))

→ Ответить

tubo28

7 лет назад, # ^ |

My way:

guess that any palindrome is bad and any non-palindrome is good (and unique)
code a solution using Manacher's algorithm
fail last sample (answer: 54)
print all strings my solution generates
find out why some are the same
look for a way to find pairs of same letters in same distance from given pivot (yay for overcomplicating)
give up, switch problem
return to it, start from scratch but no clue
finally time is up

→ Ответить

I_love_Tanya_Romanova

7 лет назад, # ^ |

+78

Oh, that 54 is familiar :D I was afraid I'm the only one here, facing side effects of droptable coaching me for ICPC :)

I really loved this problem — it made me feel stupid, then I had to guess solution from standings (there are not so many simple things you can do with string in 2 minutes), and then after figuring out why is it correct (only after the contest) I was amazed how simple&obvious it is.

It is also funny how it uses some simple but not worn-out idea, but everybody goes into palindromes because they have been hyped a bit over last years :)

→ Ответить

ipul23

7 лет назад, # ^ |

← Rev. 2 →

I also stuck with this problem , ended up by doing it bruteforce(print out all of the same strings with different left and right) and finally got it xD

→ Ответить

johnchen902

7 лет назад, # |

← Rev. 5 →

+105

I have an easy solution to E in O(n²) with a sufficiently small constant, without using NTT, unlike 998244353 suggested. (~~p.s. I didn't bothered to check other solutions.~~ It appears that first solvers have the same solution.)

int solve(int x, int y) {
    dp[0] = 1;
    for (int i = 1; i <= x; i++)
        for (int j = 1; j <= y; j++)
            dp[j] = (dp[j] + (long) i * dp[j - 1]) % mod;
    int ans = 0;
    for (int i = 0; i <= y; i++)
        ans = (ans + (long) dp[i] * inv[x + i]) % mod;
    return (long) ans * fac[x] % mod * fac[x] % mod * fac[y] % mod * fac[x + y] % mod;
}

We first observe that any valid swap is either:

Swapping a (0, 1) with a (1, 0) (swapping a_i, a_j s.t. (a_i, b_i) = (0, 1), (a_j, b_j) = (1, 0))
Swapping a (0, 1) with a (1, 1)
Swapping a (1, 1) with a (1, 1)

Let x be the number of (0, 1) and y be the number of (1, 1). Clearly the number of type 1 swaps is x, and the number of type 2 or 3 swaps is y. As type 3 swaps do not interfere with other types, we assume there are y - i of them, multiply the answer by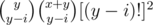 $\text{[math]}$ , and forget their existence.

Now we're left with x of (0, 1), i of (1, 1), and only type 1 or 2 swaps. Let g(x, i) be the number of possible swap sequences. Clearly,

$\text{[math]}$

Let g(x, i) = (x!)²(i!)f(x, i). Then clearly,

$\text{[math]}$

And for the final answer, we must sum over 0 ≤ i ≤ y, i.e.

$\text{[math]}$

→ Ответить

Um_nik

7 лет назад, # ^ |

+10

I think that tourist knew about this solution and made constraints lower for this to pass. If the only intended complexity was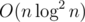 $\text{[math]}$ then why n is not up to 10⁵?

→ Ответить

johnchen902

7 лет назад, # ^ |

← Rev. 2 →

+10

Better ask tourist directly for the reason.

Anyway, I'd still post the comment as long as most of the world didn't know about this solution.

→ Ответить

tourist

7 лет назад, # ^ |

+64

Thank you for describing your solution! It's quite different from the editorial, so it's definitely worth explaining.

Indeed, we had only $\text{[math]}$ intended, but shortly before the round discovered that it's nearly impossible to separate it from O(n²). Thus, we decreased the constraints to make it obvious that O(n²) works.

→ Ответить

majk

7 лет назад, # ^ |

← Rev. 3 →

+11

It took a lot of work, but I was able to squeeze in a solution of F in $\text{[math]}$ .

Let's first consider the case where N = M, and compute A[x] — the sum of the results over all possible Yes/No sequences. Clearly, A[0] = 0.

We model the Yes/No sequence as lattice path from (N, N) to (0, 0). What happens at point (x, x) for x > 0? There will surely be a point where the path crosses the main diagonal again for the first time, that is, we reach state (y, y) for some 0 ≤ y < x.

How many ways to do this are there, and how good they score? Let's assume that the we guess incorrectly at (x, x) and we move to a state (x - 1, x). Then, our path continues to (y, y + 1) and then continues to (y, y). It is the first time we reach the main diagonal, thus the path never crosses the "+1" diagonal. There are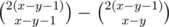 $\text{[math]}$ such paths. Since it is optimal to always guess the answer which has the most occurrences left, it is easy to see that this path scores exactly y points, plus whatever we expect to get from the path between (y, y) and (0, 0).

Similarly, if we guess correctly at (x, x), we have the same amount of paths to (y, y), but we score one more point (the one at (x, x)).

This combined yields the following recurrence: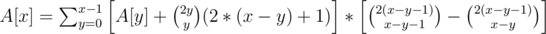 $\text{[math]}$

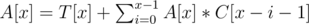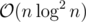The second summand in the large sum times the right term can be computed first by a simple convolution. The term with A[y] can be then computed using linear convolution (of form $\text{[math]}$ ) in $\text{[math]}$ time.

This yields 1500 points and fits quite comfortably into TL. To extend this to a full point solution, we need an extra linear step: for every point (x, x) we calculate how many paths there are for which this is the first point on the main diagonal from the path from (N, M) (again by using the above formula for lattice paths above the diagonal) and for each of them add M - x points to A[x].

The TL is very tight in this case, so one needs to have solid NTT implementation, and when doing the linear convolution using Divide & Conquer algorithm (described here), one needs to cut-off the recursion at around 2⁶.

My quite convoluted (pun intended) solution: link

EDIT: The editorial seems not to be present anymore, so I wasn't able to verify how much my solution matches it :)

→ Ответить