Закончился интернет-тур олимпиады, предлагаю здесь обсудить контест. Как решать 5ю?
→ Обратите внимание
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 156 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 23.11.2024 18:51:43 (i2).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











Как решать 8-ую?
просто моделируя аккуратно, лонг даблах, ее перетистировали если что
Там и просто в double заходит. Мы увидели столбик минусов по ней, пошли что-то придумывать и писать в рациональных дробях, но это конечно TLE.
Потом just for lulz отправили в даблах и получили AC.
А как же на тесте:
? Насколько я понимаю, правильный ответ 1 0, а на long double решение выдает 0 0.
Мда, вообще тупо получилось. Я постоянно получал ВА по задаче 8, даже написал точное решение в целых числах и оно тоже валилось на 7 тесте. А за 30 минут до конца, продолжая что-то по ней пихать, сделали реджадж и прошла попытка еще на 98 минуте. В итоге, времени ни на что не хватило. Кстати, судя по всему, у тех, кто получил АС в самом начале, решения неправильные, но просто АС не снимают.
UPD: спрятал, т.к. контест продлили
UPD2: вернул обратно
Там для кого-то еще контест идет!
После окончания контеста расскажите как решать 9
кажется уже самому пришла идея:-)
Я правильно понимаю, что сначала нужно запустить обход в глубину из любой вершины, затем запустить обход из самой отдалённой?
это верно для дерева. здесь достаточно перебрать все клетки в качестве начальной и запустить из каждой обход в ширину.
я так и делал.. TL 13
Там действительно bfs из любой вершины, а затем bfs из самой отдаленной, другие мои решения TL 13 получали.
блин, я два часа её пихал)) а после контеста пришло в голову решение) обидно
ну он говорил не про bfs, а про dfs. А описанный мной способ заходил.
а ты на чём писал? java или c++
с++
спасибо,
Ну это неправильно, например, для следующего теста:
Если запускать BFS из верхнего левого угла, самой отдаленной вершиной будет (3, 3), а от неё дальше всех снова (1, 1). В то время как правильный ответ — пометить вершины (1, 3) и (4, 1).
Можно было запускать этот процесс от случайной вершины до тех пор, пока есть время.
У нас зашел bfs не из произвольной, а из последнего # (последний символ # в последней строке)
UPD: всего 2 bfs (из последнего символа) и из самого далекого для него
Не используй STL и все отлично заходит)
TL13 лечился избавлением от стандартного queue и использованием массивов.
я вектор писал вместо очереди
а мне вот пришлось ещё цикл ручками раскручивать, чтобы зашло
А нам пришлось расписывать одномерную индексацию.
У меня нормально с queue зашло.
UPD. Вот код http://pastebin.com/njK9hyJT.
У нас прошло такое решение: Делаем BFS из произвольной вершины, запоминаем все, на которых поиск в ширину заканчивался (т.е. не было непосещенных соседей), а потом по 1 BFS для каждой из этих вершин.
Скорее всего это значит, что у авторов слабые тесты. Потому что такой финт всегда работает только для деревьев, а контрпример для произвольных графов должно быть несложно "уложить" на решетку.
Тут много комментов по поводу того, как люди получали TL. Я запусках обход в ширину из каждой вершины, и все зашло сразу же... Вот код (вроде написан довольно лаконично и понятно): (спойлер)
Расскажите, пожалуйста, как решалась А?
Например хэшами, с бинпоиском по длине ответа. Получалось что-то типа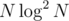
У нас валились хэши с сетом. В итоге я написал свою супермегахэш-таблицу, которая работает примерно за O(1), AC.
А можно подробнее. Писал тоже самое, но вот быстро найти аналогичную подстроку не смог
Мы делали так: Строили два массива хэшей: для двух строк В каждом хэш префиксов строки
Затем бинпоиском перебирали ответ (в общем случай от 0 до n)
Строили мапу для второй строки: map<int64, int> mp где ключ — собственно хэш значение — позиция самой левой подстроки с таким хэшем (надо чтобы строки были непересекаемые) Мапа заполняеться значением хэшей подстрок для второй строки
На каждом шаге бинпоиска за линию (O(n)) проверяем есть ли две одинаоквых подстроки начинающих в позиции i:
Пусть текущий хэш первой подстроки h1, то достаточно сделать нечто такое: mp.find(h1) и если мы нашли такой хэш, то текущий шаг бинпоиска (медиана) — подходит, шагаем в бинпоиске в правый отрезок, иначе в левый.
Итоговая сложность: log(n) — бинпоиск n — построение мапы n — перебор всех позиций начада подстроки в строке 1 log(n) — поиск в мапе Итого: log(n) * (n + n*log(n)) = O(n*log^2(n))
P.S. будут вопросы — пиши
Да нет, понял даже, как адаптировать к простому бинпоиску с хешами и мапой, попробую сдать, если будет возможность.
P.S. Просто суффиксный массив строить не умею
Лично я тоже не умею, поэтому это и писали P.S. такое решение ловить TL
Оптимайз: 1) обьявить 20 мап (чтоб не дестрактить) 2) Мапы обьвлять указателем аля (int * num;)
Я так подумал, что если мапа у нас будет такая: ключ — хеш, значение — пара из позиции начала и позиции конца. При проверке одинаковых хешей, нужно будет проверить их на отсутствие пересечений. Вроде даже можно доказать, что нам достаточно хранить первое вхождения хеша. Что-то типа: Предположим, что это не так, тогда для того, чтобы найти ответ, нам нужен хеш, который начинается либо после нашего хеша, либо пересекается. Если он находится после, то тогда храня первое вхождение, мы, найдя вхождение следующего хеша, и так поймем, что они не пересечены, и мы нашли ответ. Если же нам нужно хранить хеш, который имеет пересечение с первым хешем, то тогда, найдя для него ответ, несложно заметить, что ответ так же не пересекается с первым хешем, так как позиция начала ответа > конца второго хеша > конца первого вхождения. Кривовато написал, но вроде достаточность хранения первого вхождения хеша доказал.
Я написал за O(N * log(N)), использовав хешмапу.
Также можно хранить не самую левую подстроку, а просто количество подстрок с таким хешем. На каждой итерации заполняем мапу хешами подстрок 2 строки, начиная с подстроки [len..2 * len — 1] (len — проверяемая длина). Теперь пройдемся по подстрокам первой строки, на каждой итерации просто уменьшая на 1 значение в мапе для того хеша, который мы начинаем пересекать. Если в какой-то момент мы найдем хеш, для которого в мапе будет ненулевое значение — для такой длины подстроки существуют.
Честно говоря не понял зачем на кол-во подстрок.
А насчет поиска хэша в мапе: юзал find?
1) Мы храним количество подстрок, чтобы при переходе к следующему хешу в первой строке быстро убрать тот хеш второй строки, с которым мы начинаем пересекаться. Для этого мы просто уменьшаем количество таких хешей на 1. Соответственно, значение 0 в мапе для хеша означает, что таких хешей в оставшейся части 2 строки нет.
2) Я писал на яве, поэтому find не юзал)
В нашем случае — суффиксным массивом.
У кого был WA17?
Интересно, когда разморозят монитор?
разморозили
А можно ли в 6 просто найти моменты времени, когда каждая вершина покидает / попадает в конус и на этих интервалах устроить тернарный поиск? Внутри интервала у фигуры будет меняться только та часть площади, которую дают 2 крайних треугольника.
Кто-нибудь знает что такое WA 8 в 10-ой задаче?
Погрешность, мое решение зашло бы таки если бы успел послать )) Последняя попытка просто переполняется инт :) Там суть в том чтобы совсем везде убрать даблы
У нас все в long long. Кроме цены в евроцентах за 10 - 5 литра. Не ужели тут падает на одной покупке?
У нас на контесте было WA12.
Как 7 решать, чтобы обойти погрешности?
Целочисленно. Всмысле домножить данные на 103. Там все в long потом уместится.
А мы сегодня узнали, что, оказывается, числа бывают отрицательные, и они округляются немножко по другому, т.е. вместо ll(x*100000 + eps) надо писать ll(x*100000 — eps)
А лучше писать вобще round() ;)
10^3??? там же вроде 10^-5 точность была.
Не я писал задачу, так что точно не помню. Но помню, что умещалось все.
Там кажется итак проблем не возникало, по крайней мере в лонг даблах.
А кто знает, как выводить формулу в задаче 2? Я, например, физику не знаю и подобрал ответ чисто исходя из размерностей. Но все-таки хочется узнать нормальное решение.
очень просто, очевидно ускорение направлено вверх, т.к. нить изначально натянута и вертикальна, соответственно запишем теорему пифагора для малого участка времени(т.е. по сути напишем закон сохранения длины веревки) y2 + (vt)2 = h2, где y, координата нашего чувака, и продифференцируем дважды, подставим t = 0 и получим счастье.
ADD: А можно сразу воспользоваться известным фактом, что центростремительное ускорение при движении по окружности равно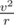
Мы вот долго не могли понять, почему ответ не сходится, а там оказывается скорость была в км/ч.
Аналогично =)
Может кто-нибудь в тренировки CF выложить этот тур пожалуйста?
Кто-нибудь знает, что такое WA17 по задаче 5? Или может сможете указать ошибку в моём коде в правке.
Тест:
О ужас :) Спасибо.
Как решать 3?
Легко понять, что все функции, выражающиеся через F — это монотонные (по каждому аргументу) и равные 0 в 0.
Таких всего около 7000 и можно для всех них генерировать ответы в порядке увеличения длины.
Чтобы это работало за 7000^2, а не 7000^4, нужно генерировать F в два этапа: отдельно пытаться получить все новые функции вида F1 & F2, а из пар полученных таким образом функций делать F1 | F2.
примерный код
Черт, а я убедил сокомандников, что монотонных функций много >_<
Спасибо!
Нам ещё пришлось часть предподсчитать...
Что такое "Тренировки", и как в них зайти?
1) Заходим на страницу регистрации.
2) Выбираем раздел "Тренировки".
3) Заполняем поля, нажимаем кнопку "Отправить".
4) Логинимся в систему, дальше будет либо выбор олимпиады (где нужно выбрать "Тренировки"), либо сразу откроется нужный раздел. Выбор будет только в том случае, если один и тот же логин зарегистрирован в нескольких олимпиадах, иначе — раздел откроется сразу.
Спасибо большое!
так как все таки решать 5ю?
Как решать задачу без конфет, т.е. все bi фиксированные: для каждого элемента первого типа и для каждой комнаты посчитаем вероятность с которой этот предмет в конце возьмется. Сумма вероятностей по всем предметам это матожидание. Вероятность что предмет перейдет в следующую комнату c[i] / (a[i] + b[i] + c[i — 1]). К этой идее достаточно просто прикручивает возможность добавления к b[i] некоторого числа. В итоге динамика такая — минимальное матожидание для первых i комнат и еще осталось j конфет.
Как решать J?
Мы сдали динамику:
Состояние -- количество топлива в баке и номер заправки.
Значение -- затраченная сумма.
При этом рассматривались только достижимые состояния: известно, сколько топлива потратилось на пути к этой заправке, а закупать можно только кратное 0.01 количество. Учитывая ёмкость бака, состояний на одной заправке получается <=5000
Переходы такие:
1) "Залей-ка мне ещё 0.01 литр этого топлива."
2) "Округляй мои деньги и гони до следующей заправки!"
Всё считали в целых.
А разве не бывает случая, когда нельзя доехать просто тупо переходя к следующей заправке, потому что в какой-то момент топлива станет некратное 0.01 количество и не хватит до финиша совсем чуть-чуть. При этом если бы отъехать от заправки на eps вперед, а потом на eps назад, то это могло бы решить проблему? Я что-то не понял, как этот случай у вас учитывается или я условие совсем неправильно понял и там, например, назад вообще нельзя ездить?
Не учитывает. Действительно, в условии не запрещается такой вариант.
С другой стороны, словесное описание формата вывода намекает, что дважды заправляться на одной заправке нельзя.
Ну может быть оно и намекает, но, мне кажется, что я и очень большая часть участников до словесного описания формата вывода не дошли как раз по той причине, что поняли условие ровно так, как я :)
Просто все эти округления и разные точности разных величин в содержательной части условия, по-моему, просто заставляют попробовать поискать подвох в них, к тому же он достаточно быстро находится. Уж то, что ездить назад нельзя из условия совсем непонятно, при этом возможность езды назад позволяет сливать топлива столько, сколько нужно.
Как раз замечание о том, что сливать топливо нельзя, даёт понять, что ездить назад тоже нельзя. Потому что это уж совсем очевидный трюк для слива топлива.
К тому же, чекер к задаче в вашем понимании становится сложнее. Проще уж формат вывода было бы соответствующий сделать.
Почему получается состояний на одной заправка <= 5000? Емкость бака — 50 л. Потребление бензина — число с двумя знаками после запятой. Все расстояния — числа с тремя знаками после запятой. Т.е. за переезд от одной станции к другой может потратиться 0.00001 бензина. Итого состояний на одной станции: 50 * 100 * 1000. В чем я не прав?
П.С. Сам же и разобрался) Кол-во бензина на станции = кол-во купленного — кол-во потраченного. Кол-во потраченного для каждой станции фиксированно = Si * M, а кол-во купленного изменяется с шагом 0.01.
Как решалась 4-я?
Поддерживаю, очень хочеться узнать как решалась 4 задача (про прыжки)
Поймем, что все длины прыжка, при которых получается пропрыгать — это непрерывный отрезок чисел. У нас есть одно число из этого отрезка, давайте бинпоиском искать границы. Для фиксированной длины D проверять будем так: давайте хранить отрезок, который будет содержать все точки, с которых мы можем начать прыгать, сначала это [-infinity, x[0]]. Теперь для любого i x[i] <= start + (i + 1) * D <= x[i + 1]. Это тоже самое, что пересечь текущий отрезок с [x[i] — (i + 1) * D, x[i + 1] — (i + 1) * D]. В конце должно еще быть start + n * D >= x[n — 1], т.е. еще пересечем с [x[n — 1] — n * D, inf]. Если пересечение получилось не пустым, то такая длина прыжка подходит.
"Поймем, что все длины прыжка, при которых получается пропрыгать — это непрерывный отрезок чисел"
А как поймем? Всм можно какое нибудь доказтельство?
Ну собственно по проверке ответа можно доказать, что подходящие D — это какой-то отрезок. Первое, D — ограничено сверху условиями, что точки прыжков, должны попадать между трещинами. Теперь поймем, когда D — плохое, это значит, что какие-то два отрезка из пересекаемых не пересеклись, пусть i < j x[i + 1] — (i + 1) * D < x[j] — (j + 1) * D. Т.е. D < (x[j] — x[i + 1]) / (j — i). Еще надо рассмотреть когда x[i] — (i + 1) * D > x[j + 1] — (j + 1) * D. Из всех возможных i и j выберем максимальное ограничение, получим, что при D < D1 прыжки точно не подходят. Также можем получить D2, при D <= D2 ответ есть. Вот и получаем, что все D — это отрезок. Не очень строго конечно =)
Весьма печально, когда смена double на long double дает AC по задаче, которую так и не сдал на олимпиаде..
не стоит огорчаться, убогая задача, что с нее взять
Кстати, я про 7ую (: даже если так, приятнее, когда она все же сдана)