Be F(N, K) = 1^k + 2^k + 3^k + ... + n^k.
Given N and K we need to calculate F(N, K) (mod 2^32)
INPUT:
1 <= N, K < 2^32
PS: I think about this question for a few days and didn't get success if you have any idea how to solve it, please share it :D
The problem can be found here to submit (statement in portuguese): http://olimpiada.ic.unicamp.br/pratique/programacao/nivels/2013f3p2_somapot











Here's a similar question with editorial from HackerRank , unfortunately in the editorial the solution run in O(k), and probably will not pass here. I don't have a solution yet (i tried a lot too), but maybe this can help somehow. The solution presented in the editorial uses modular inverse and this will be a problem to consider too.
btw , expected time limit is 1 sec according to judge.
PS : Someone correct me if i'm wrong, but using Lagrange Polynomial or Bernoulli Numbers for solve this is out of question since B(2) don't have any inverse mod 2^32 and one can prove that same thing can happen with Lagrange Polynomial for sure for some values of K.
If k < 32, use matrix exponentiation.
If k ≥ 32,
1k + ... + nk
and it reduces to the previous case.
Why did you replace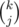 with
with 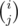 ? But even then, I can't see how to evaluate
? But even then, I can't see how to evaluate 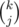 mod 2^32.
mod 2^32.
Since j is small ( < 32) you can "walk on the line" of the pascal triangle.
You can cancel the 2's that show up in denominator with the ones that appear on the numerator.
I am not sure, cancelling the 2's is fine but that doesn't mean the intermediate values will fit in the available data types. I am guessing you keep cancelling the 2's and take modulo inverses, is that correct?
To be clearer, my idea is to remove all 2 factors from the divisors and calculate the multiplicative inverse with extended Euclid algorithm.
Not sure if that is the most elegant way, but it'll do it.
Got it, thanks!
The most straightforward way is to use BigInteger.
(Since j is small,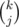 is not too big.)
is not too big.)
Can you please elaborate how to find binomial coefficients fast mod 2^32 and how to use matrix multiplication here? Thanks.
Write
Convert this to matrix and use exponentation.
Awesome! Very clever trick to exploit the relation between summations removing the first, not the last element. Thanks!
Thank you, i understand now.