Всем привет!) Расскажите пожалуйста как решались задачи с минувшего четвертьфинала в Санкт-Петербурге (4 ноября). Интересуют F, G, H.
→ Обратите внимание
До соревнования
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
5 дней
Зарегистрироваться »
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
5 дней
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 156 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | nor | 152 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 25.11.2024 23:57:41 (i1).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











Which division you are considering?
Div1 problems: https://neerc.ifmo.ru/archive/2017/northern/north-2017-statement.pdf
Div2 problems: https://neerc.ifmo.ru/archive/2017/kazakhstan/northern-lite-2017-statement.pdf
Div1
I also want to know their solutions, also problem D. (thought D of div2 was pretty easy, but seems there are very few teams who solved D in div1)
I did not read this problem) We will wait for tutorial together)
Помогите пожалуйтса с задачей L. Какие могут быть частные случаи. Получаю WA на 19-ом тесте
http://neerc.ifmo.ru/archive/2017/northern/north-2017-analysis.pdf
А был где-нибудь видео-разбор? Из презентации мало что понятно.
Я тоже хотел бы найти полный текстовый/видео разбор. Но пока нашлась только эта презентация.
Есть надежда что кто-нибудь сюда заглянет своим решением поделится)
Разбор должен был быть, но из-за задержки соревнования решили сразу преступить к разморозке/награждению.
Там ещё есть архив с решениями от жюри, может он поможет.
Построим какой-то ДФСный остов. Предположим, что S — предок F (доказать можете сами почему это так), тогда ответ есть тогда, когда из двух вершин из поддерева вершины F есть обратные ребра (хотя бы 2) вне остова, которые идут в вершину, в поддереве которой лежит S. Как это писать: каждой вершины V будем считать minH — минимальная высота вершины, в которую ведет обратное ребро из любой вершины поддерева V. Тогда обрабатывая вершину V она станет F, если есть 2 вершины (и вероятно она сама — тут нужно быть аккуратным), у которых minH < h[V].
Что бы мы делали, решая задачу для одного дерева? Откусывали бы от дерева пару лист-предок, пока это возможно. Давайте от каждого дерева из леса сделаем эту операцию. От каждого дерева останется список вершин, которые не попали в пару. Теперь давайте отсортируем деревья по компаратору "сначала все у которых рут в паре, а после по убыванию свободных вершин". Теперь будем жадно добавлять деревья в этом порядке, поддерживая множество свободных вершин (если рут текущего дерева свободен, попробуем его замапить к одной из свободных, иначе к главному боссу).
F.
Нам гарантировалось, что все циклы строго вложены и есть ровно один lag.
Каждый цикл имеет форму
for i in range(j, k)Из этого следует, что j ≤ i, i ≤ k. Построим из переменных в циклах граф, каждое ребро в таком графе соответствует отношению ≤ (если i = 1 или k = n, то соответствующее ребро опускается), нужно посчитать число способов выбрать каждую переменную от 1 до n, чтобы граф отношений был корректен.
Общий случай, если в графе нет циклов. Предположим, что граф задаёт линейный порядок на элементах, тогда ответом является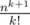 . Если не задаёт линейный порядок, то нужно домножить на число линейных порядков соответствующих нашему частичному. Это количество топсортов в графе, что считается динамикой по подмаскам.
. Если не задаёт линейный порядок, то нужно домножить на число линейных порядков соответствующих нашему частичному. Это количество топсортов в графе, что считается динамикой по подмаскам.
Особый случай если в графе есть цикл. Тогда все эти переменные равны друг другу, можно этот цикл сжать и запустить решение от меньшего графа.
G.
Рассмотрим остов DFS. Каждое ребро вне этого остова порождает некоторый простой цикл в исходном графе, причём каждому такому циклу соответствует какой-то вертикальный путь в дереве.
Если существует два таких dfs-цикла, пути которых пересекаются по хотя бы одному ребру, то они образует ответ (общая часть является одним из путей, две другие берутся из циклов), если таких нет, то наш граф является кактусом, в нём ответа нет.
Как проверить и найти пересекающиеся пути? На самом деле достаточно просто. Для кажого ребра остовного дерева будем сохранять допрёбра, проходящие через него. Когда мы в dfs-е обнаруживаем допребро (и ему соответствующий цикл), то явно проходим по каждому ребру в пути соответствующему этому циклу и добавляем дополнительное ребро в соответствующий список.
Если после добавления в списке окажется 2 дополнительных ребра, то вот оно пересечение.
Время работы линейное, так как в каждый список добавим ≤ 1 элемента.