arjun95's blog

Discrete logarithm over composite modulus
By arjun95, history, 7 years ago, In English

how to solve discrete logarithm over composite modulus, i know over prime modulo using Baby-step giant-step algorithm, but in case of composite modulus i have no idea how to solve this. i think this can be done by factorization of modulo and chinese remainder theorem but i don't know how to do this.

  • Vote: I like it
  • -1
  • Vote: I do not like it

Comments Comments (12)
| Write comment?
»
7 years ago, # |
  Vote: I like it -8 Vote: I do not like it

As far as I understand, you want to solve the equation . If 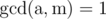, you can use baby-step giant-step algorithm.

Let m1 be product of all prime powers pk such that pk|m and p|a. m2 = m / m1. By construction m1 and m2 are coprime. For sufficiently large x (at least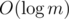 ) 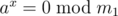. Check the small values separately.

If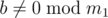 , there are no solutions. Otherwise we need to solve the equation modulo m2. 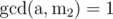. This case has been analyzed above.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    can you elaborate the calculations of m1.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      m is product of some powers of primes piki. Some of these primes divide a, some don't. m1 is a product of those powers for which pi divide a. m2 is a product of other powers.

      For example, if a = 60 = 22·3·5, m = 126 = 2·32·7, m1 = 2·32 = 18 (2|a, 3|a), m2 = 7 ().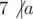

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it +1 Vote: I do not like it

        thanks for your explanation.

        but for your given example, a = 60, m = 126, for b = 18, answer should be 4, but after calculation of m1 and m2, m2 = 7 which gives value of x = 1 then how to come up with final solution(x = 4), correct me if i'm wrong

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Nice example. That's why we should care about small values of x.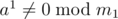 , but for all x ≥ 2 .

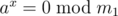          If x is too small, we can look at x + tφ(m2).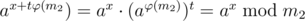 . For sufficiently large t we get .

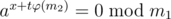          In this example φ(m2) = 6, so for t = 1 we find x = 7.

          → Reply
          • »
            »
            »
            »
            »
            »
            7 years ago, # ^ |
            ← Rev. 3   Vote: I like it 0 Vote: I do not like it

            thanks for such a nice explanation.

            but if we have to find smallest value of x (which is equal 4 in above example) then how it can be calculate.

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              7 years ago, # ^ |
                Vote: I like it 0 Vote: I do not like it

              Did you know how to do it if m is prime? In the same manner we can find the smallest x such that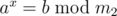 and x is large enough (). It remains to check small values of x.

              → Reply
              • »
                »
                »
                »
                »
                »
                »
                »
                7 years ago, # ^ |
                  Vote: I like it 0 Vote: I do not like it

                no, i don't know how to calculate smallest x when m is prime.

                → Reply
                • »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  7 years ago, # ^ |
                    Vote: I like it 0 Vote: I do not like it 
                  map<int, vector<int>> pows;
int k = sqrt(m);
for (int i = 0; i <= k; ++i)
    pows[Pow(a, k * i)].push_back(i);
for (int i = 0; i <= k; ++i)
    find something in pows[b * Pow(a, i) % m]

                  If we want to find the smallest solution modulo prime, in the last line we just choose the smallest element from this vector. In our case we need to do some binary search here.

                  → Reply
              • »
                »
                »
                »
                »
                »
                »
                »
                7 years ago, # ^ |
                  Vote: I like it 0 Vote: I do not like it

                Can you explain the reason for the inequality ?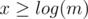

                → Reply
                • »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  7 years ago, # ^ |
                    Vote: I like it +1 Vote: I do not like it

                  If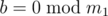 , we want to get 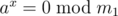. It means that for each prime p its power in ax is not less than its power in m1. Power of p in m1 is at most 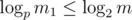. On the other hand, if 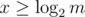, power of p in ax is at least .

                  → Reply
              • »
                »
                »
                »
                »
                »
                »
                »
                5 years ago, # ^ |
                ← Rev. 2   Vote: I like it 0 Vote: I do not like it

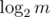                I still didn't get how can we combine the powers obtained when divided by $$$m_{1}$$$ and $$$m_{2}$$$ individually to get the power when divided by $$$m = m_{1}*m_{2}$$$. Can you please explain that?

                Also, why is this post getting downvotes. Is there something wrong with the solution described in the comments section?

                → Reply