AlexanderBolshakov недавно привел ссылку на замечательную задачу: номер 4 отсюда. Прекрасная задача, всех призываю над ней подумать и, если придумаете, запрограммировать. Давайте, чтобы было чуть-чуть понятнее, что происходит, я попробую погрузить ее в некоторый контекст.
- Что если вместо манхэттэнского расстояния будет евклидово? Станет ли задача проще или сложнее?
- Что если мы хотим приближать нашу метрику манхэттэнским расстоянием, но знаем, что метрика наша не абы какая, а получена как попарные евклидовы расстояния между некоторыми точками в многомерном пространстве?
- Теперь рассмотрим обратную ситуацию: у нас есть метрика, которая получена взятием попарных манхэттэнских расстояний в многомерном пространстве, а мы хотим приблизить ее евклидовыми расстояниями?
Есть идеи?











Выглядит как сущий ад. Я в свое время пытался вкладывать транзитивные DAG-и (графы сравнений) в пространство Rk с отношением "все координаты меньше". Уже при k=2 приходится строить шаманства.
Совершенно точно, в задачах распознавания есть задача "дано N точек в Rn, вложите их в Rm (m < n) так, чтобы расстояния были похожи". И, насколько я понимаю, ничего хорошего там нет.
В общем, все зависит от деталей, а именно насколько устраивают существенно неточные эвристики (например, случайным образом накидать точки и потом эмулировать "пружинки" между ними).
First of all, sorry for English: I don't have Russian layout here, and hate translit.
One important remark: we do not care about dimensionality of the image. So, if we can embed our metric into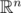 very well for a large n, then this is not a problem.
very well for a large n, then this is not a problem.
Your notion of "monotone embedding" is interesting: I'll try to think about it.
The "dimension reduction" paradigm is actually well-studied: for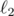 there is a celebrated positive result — Johnson-Lindenstrauss Lemma, for
there is a celebrated positive result — Johnson-Lindenstrauss Lemma, for 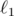 there are several negative results (see, e.g., here).
there are several negative results (see, e.g., here).
Heuristics are nice, but the puzzles from the post do not require anything like this.
P.S. Do you know how to solve the problem from the MIT contest?
Лемма замечательная, не знал, правда, насколько я понимаю, вложение в ln(число точек) не особо интересны, интересны n = 2..4 и хоть какой-то результат.
В задаче натолкнулся на ошибку интуиции вида "любый взвешенный граф с неравенством треугольника может быть вложен, ну в Евклидово-то точно". Постановка из поста неявно противоречит этому, так что в глубоких раздумиях.
На контесте с такими задачами проще:
Самый простой пример графа, который не вкладывается изометрически в евклидово пространство -- цикл длины 4, более общо -- куб любой размерности.
Кстати, вот первый тест, на котором кэпское решение валится:
Ответ:
P.S. Куда лучше залить остальные тесты? Могу на какой-нибудь файлообменник вроде депозита, но, может быть, есть что-то поприличнее?
А вы разобрались, как задача решается?
Если бы разобрался, я бы не писал, что мне интересно узнать, как она решается :).
Я смог только выполнить очевидное сведение к метрике, в которой дистанция выражается как max(|ax1 - bx1|, |ax2 - bx2|, ..., |axn - bxn|)
Да, ответ на закономерный вопрос: тест я взял из ижевского архива.