What is better than setting one AtCoder Grand Contest? Setting two AtCoder Grand Contests, of course!
AtCoder Grand Contest 020 will be held on Sunday (time). The writer is tourist.
This is the first contest of 2018 counted towards AtCoder Race Ranking. If you get into top 30 in this contest, you will get GP30 scores.
The point values will be 300 — 500 — 700 — 1100 (500) — 1400 — 2100. Note that the contest duration is unusual (130 minutes).
Let's discuss problems after the contest.










What is better than setting two AtCoder Grand Contest? Participating in two AtCoder Grand Contests held by tourist, of course!
Previous AGC set by tourist was 4,5 months ago, it's kinda hard to believe but these two AGCs are two AGCs in a row xD. Glad to see AGCs coming back (next one is scheduled three weeks after this).
Isn't the next one three weeks after this and not two?
Indeed, thanks for nice catch, I will correct it
Pls kill me, I forgot about it and slept too long >_> Moreover before changing timezone AGC was always at 2PM, but now it is at 1PM, so it was 13min versus 1h13min being late in my case xd
Hm so the takeaway here for me is that you sleep past 1pm. Impressive.
1pm? These are rookie numbers
Judging from your personality, I thought you were trying F.
Score for D: 1100(500) means? is 500 partial score like in Codechef?
1100 (500) means that the full score of problem D is 1100, but it's possible to get 500 points for solving the problem for partial constraints mentioned in the problem statement.
It is unfortunate, I wasn't able to submit in last 2 minutes, page just didn't want to load :( You maybe should have extended the contest for 5/10 minutes because of such issues.
What is the solution to problem F?
I found the solution to the case where all L's are equal here, but the obvious generalization to the case where L's can be different was incorrect.
Uploaded the editorial.
Thanks. I've already seen it. By the way, why is there no subtask for solving the case where all L's are equal?
Well, the fact that it's searchable on the Internet is a good counterargument.
It seems that we can speed up editorial solution a little by using one more bitmask in the dp state, instead of generating all (N - 1)! permutations..
Nice, you are right, we didn't notice that. In fact, 5! < 25·5, but the complexity becomes O(22N - 2·N3·C2).
Solution for C?
I solved by using bitset. O(n2 × a) DP is obvious but if I use bitset seems like we can achieve O(n2 × a / 64). Is it true that bitset is always very fast in use of bitwise operation?
Something else that passes is probabilistic solution of shuffling array and then assuming that optimal solution likely never has delta at any time exceeding 50000 (that is when we are solving problem of partitioning array into two halves as close in sum as possible, in our dp we can limit current delta between halves to [-50000, 50000]).
The delta between halves is at most 2000 because if it exceeds, we can move one element from the larger side to the smaller side and get a better solution.
So this makes sense for the final delta, however how does this help us during our dp? As in although final delta is <= 2000, the delta at when we are say midway through our dp can be greater, or is there some easy way to avoid this?
Right, I didn't get exactly what you were trying to say. In that case the delta can indeed be larger.
The final delta is indeed at most 2000, but if we add elements to halves in random order, intermediate deltas may be larger. I assume they are bounded by something like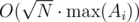 with high probability, since the process looks like a random walk.
with high probability, since the process looks like a random walk.
Can we binary search on the answer (say X) and see if exactly (2N - 1) / 2 subsequences have sum less than X? Would that work within TL?
We can use DP to check that. f(i, j) represents no. of subsequences using first i numbers with sum < j. Maintain only 2 rows in the DP table to avoid exceeding memory limit.
Numbers can get very large, on order of 2^2000, what is your plan of avoiding this? Or if you do have such large numbers, I imagine TLE.
Right, I did not consider that. Thanks.
What a coincidence... Getting AC after fraction of a second...
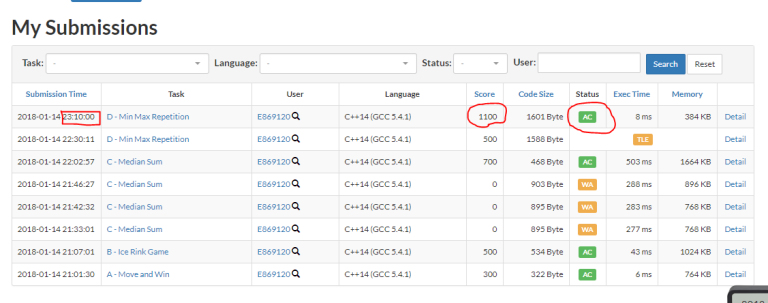
You were 8ms late
Interesting, how did you get this information?
You should ask organizers to accept this. The only thing that matters is submission time.
What makes you to make it required to use bitset in problem C? Is there any trouble if n<500?
We can calculate Dp[i][j][t] (1 ≤ i ≤ N, 1 ≤ j ≤ N·Max, 1 ≤ t ≤ C) the number of ways to have sum j using the first i elements modulo P[t] in O(N2·Max·C). We can choose P[t] (1 ≤ t ≤ C) to be a prime number ~262. Now we can find for sure the (2N - 1)th element if we choose C = 8 primes.
I'm not sure that's the reason though...
Right, we didn't want straightforward counting solutions to get accepted.
And you didn't think about slow languages such as Java or C#? (I know Python is too slow for programming contests though)
We did. Our Java solution using built-in
java.util.BitSetgets accepted in 619 ms, which is less than 1 / 3 of TL.Can you also tell why we'll be able to surely find (2N - 1)th element using C = 8 primes? That doesn't seem very intuitive to me.
Suppose you have that x ≡ 2N (mod Pt) for every t (1 ≤ t ≤ C) then by Chinese Reminder Theorem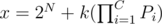 . Because we choose 2N to be smaller than
. Because we choose 2N to be smaller than 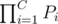 the solution is unique in our case.
the solution is unique in our case.
Why not just use big integers to compute dp?
wrong
How do you do it with fewer primes?
Oh, yeah, you're right, I feel stupid now. It's just the first that came to my mind...
Atcoder is another judge?
It's the contest of another online judge, Atcoder.
Thanks
Also there is another online judge Csacademy
What could be the worst case for problem D subask.1 ? I try q=1000 with all a=b=1000, and c=1, d=100. and it runs very fast on my computer, but I get TLE on it when submitting it.
It gives verdict on all cases combined.So if you attempt for partial you will get TLE. But the score reflects on standings page.
AtCoder Race Ranking
In problem E, I don't understand the explanation of the "Programmer's way" to figure out that the number of DP state is not large.
Suppose we are given string S as input. Then, we call f(S). Let T be any string passed as a parameter to f in a later call. It turns out that for every i,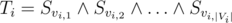 for some sets
for some sets 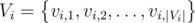 .
.
Now, instead of accepting S as input, accept only its length |S| and assume the general case. Initially,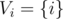 for all i. For subsequent calls of f, these sets can be formed in the same way as DP is calculated.
for all i. For subsequent calls of f, these sets can be formed in the same way as DP is calculated.
Thus:
I think I got it. Thanks for the clarification.
Just a curious question... Did you intend that many people would come up with the "Programmer's way" and "Mathematician's way" during the contest, tourist?
Of course I expected most people to come up with "Believer's way", or even just "Submitter's way" :)
I had to prove my solution in order to set this problem, though, and I came up with "Programmer's way", but I didn't expect anyone to implement it. rng_58 came up with "Mathematician's way" while solving the problem, and I think it was possible to convince oneself using similar observations during the contest.