Вступление
Недавно мне рассказали про некое «преобразование Монтгомери», которое якобы сводит вычисления по произвольному модулю к вычислениям по модулю 2k. Звучит интересно: во всяких вычислениях по простому модулю самое долгое место — как раз взятие по модулю после каждой операции. Но как именно преобразование работает, не рассказали. Повезло, что я живу в эпоху интернета и любую интересующую меня тему могу с тем или иным успехом загуглить.
Гугл рассказал, что штука называется «алгоритм Монтгомери», описана на википедии и итмошных вики-конспектах. Оба описания мне не очень понравились, потому что (хоть и объясняют, что делать) показывают гипноформулу, которая магическим образом решает нашу проблему. На вики-конспектах есть ссылка на англоязычную статью, в которой хотя бы пояснено, почему формула работает. Впрочем, пока я с этим всем разбирался, выяснил ещё пару интересных моментов, так что всем привет и поехали.
О чём речь
Задача перед нами сегодня простая: умножить два числа по модулю третьего, то есть вычислить (A × B) % N. Вот только делить с остатком мы очень не любим: в целом инструкция деления в компьютерах выполняется не очень быстро, а уж если числа длинные, то не только работает долго, так ещё и писать это нудно и сложно.
И что теперь
Фокус, который предложил Монтгомери следующий: давайте возьмём некоторое число R и будем вычислять не (A × B) % N, а (A × B × R - 1) % N. Казалось бы, добавилось ещё и деление по модулю, тоже операция не сахар. Однако, при некоторых R это почему-то значительно упростит нашу задачу.
Вот только чем это нам поможет умножить два числа? Предлагается сначала умножить числа на R, потом умножить друг с другом, потом умножить на R - 1. Действительно, перевод X' = (X × R) % N переводит сложение в сложение, а умножение — в то самое умножение с делением на R, которое было обещано раньше: A' × B' × R - 1 = A × R × B × R × R - 1 = A × B × R = (A × B)'. Википедия такое X' называет n-остатком числа X.
Оставим пока в стороне вопрос о том, как быстро переводить числа туда-сюда и разберёмся, как же делить на R по модулю N.
Гипноформула
Та самая, которая написана везде и считает что-то полезное. (Я немного наврал в ней, но скоро исправлюсь.)
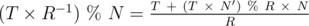
Обратите внимание, что в правой части обычное, целочисленное деление на R, никакого деления по модулю. Интересно, в какую сторону округлять? Ещё появился какой-то непонятный N', что это вообще такое?
На самом деле, формула не так уж и странна, как кажется на первый взгляд. Многие посетители сайта codeforces.com иногда решают задачи по спортивному программированию, в некоторых таких задачах надо выдать ответ по модулю 109 + 7, а порой в промежуточных вычислениях приходится делить на два. Как же разделить число на два по модулю 109 + 7? Если число чётное, то взять и разделить, к нечётному прибавить 109 + 7 (получится чётное) и тоже разделить.
В гипноформуле такой же фокус, просто обобщённый. Мы к числу T прибавим нечто, умноженное на N (остаток по модулю не изменился) и поделим на R. Если мы подберём нечто так, чтобы деление на R произошло без остатка (вот и ответ на вопрос про округление), то получим почти правильный ответ.
Где взять нечто
На самом деле, у этой формулы есть брат-близнец. Нам нужно вести одновременное вычисление по двум разным модулям — ровно это было в КТО. Пришла пора выяснить, что такое N'. Википедия и конспекты предлагают брать его из формулы 1 = N × N' + R × R' 1 = R × R' - N × N', то есть из расширенного алгоритма Евклида для N и R. Идея хорошая, но для понимания мне было проще считать, что N' = ( - N - 1) % R (эквивалентность этих двух N' остаётся читателю в качестве упражнения). То есть, числитель гипноформулы, вычисленный по модулю R выглядит как T + T × ( - N - 1 × N) = T - T × 1 = 0. И правда, делится на R. Кстати, это даёт нам первое ограничение на R: оно должно быть взаимно просто с N.
Где я соврал
По формуле получилось, что мы вычислили правильный ответ по модулю N. Может быть, получилось и правда нужное нам число. А может быть, с добавлением 15763 × N, и теперь всё равно придётся брать по модулю. С тем же успехом можно было просто вычислить A × B и сказать «это ответ, держите». Но не совсем.
Давайте оценим что получилось, считая, скажем, что 0 ≤ T < N2 (как это обычно и бывает после умножения двух чисел). Как известно, (T × N') % R < R. Остаток по модулю вообще всегда меньше модуля. Числитель в формуле меньше, чем N2 + N × R, а его потом ещё и на R поделят. Уже видно, что если R > N, то результат будет меньше 2 × N. То есть после применения гипноформулы, конечно, надо ещё взять по модулю, но это «взятие» — одно сравнение и, возможно, одно вычитание. На вики-конспектах так и написано: if (u >= n) return u — n;
С помощью нехитрого if'а мы починили формулу, получили правильный ответ и второе ограничение на R: оно должно быть больше, чем N.
Шило на мыло
Взятие остатка по модулю N заменилось на деление на R, и ещё взятие остатка по модулю R в числителе формулы. Где же польза, если мы всего лишь одно деление заменили двумя другими? Фокус в том, что мы сами выбираем R и можем подобрать такое, делить на которое — одно удовольствие. Степень двойки, например. Или, если у нас длинная арифметика с каким-то основанием, то степень этого основания. Тогда остатки по модулю и деления превратятся в сдвиги и выкидывание лишних цифр.
Подведём итог
Получилось, что аккуратно выбрав R (например, минимальное 2k > N) мы научились без деления вычислять (A × B × R - 1) % N. Для этого нам надо заранее вычислить N' — один раз для каждого модуля. Ещё нам может пригодиться RN = R % N, и, кажется (на самом деле нет), R - 1 % N. Зато на самом деле ещё понадобится R2 % N (впрочем, не всегда).
Дальше вики-конспекты утверждают, что для умножения это не очень полезно (наглая ложь — см. ниже), зато полезно для возведения в степень. И правда, при возведении в степень нам надо один раз перейти от числа к его n-остатку, уже его возвести в степень, по полученному n-остатку ответа вычислить настоящее значение ответа. Честное деление для перевода туда-сюда использовалось всего дважды, а вот умножения внутри возведения в степень все быстренькие, монтгомериевые.
Ещё лучше дела обстоят, например, с тестом Миллера—Рабина, проверкой числа на простоту. Напомню, там надо было:
- Разложить P - 1 = U × 2K
- Сгенерировать случайное число X. (Кому оно надо? Сгенерируем сразу n-остаток.)
- Возвести его в степень U. (Получим n-остаток возведённого, переводить в обычные числа лень.)
- Сравнить с единицей. (Упс. Ну ладно, сравним с n-остатком единицы, то есть с RN.)
- Возводить в квадрат, попутно сравнивая с 1 и -1. (Ну вы поняли, продолжаем держаться в n-остатках, сравниваем с RN и P - RN).
То есть, в некоторых случаях вообще не приходится переводить числа в n-остатки и обратно. Впрочем, так ли это сложно?
Скажем, по n-остатку X' надо вычислить обычный X = (X' × R - 1) % N. Надо ли брать по модулю? Конечно, нет. И умножать ничего не надо, и даже вычислять R - 1 % N — лишнее. Потому что делить на R по модулю N — ровно то, что делает гипноформула, надо просто применить её ещё один раз к результату.
С переводом числа в его n-остаток сложнее, но не сильно. Здесь-то и пригодится предподсчитанный R2 % N, ведь (X × R) = (X × R2 × R - 1), а это мы уже умеем считать по гипноформуле. То есть, в переводе чисел к n-остаткам и обратно тоже не нужно взятие остатка по модулю, достаточно применить умножение Монтгомери ещё пару раз.
Вот и сказочке конец
А кто слушал — может ещё почитать, как я простые числа ищу.
$ cat primes.in
100000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
100000000000000000000000000000000000000000000000000000000000000000000000000000000000000000010000
$ g++ -Ofast -Wall -Wextra -Werror -o primes -x c++ primes.c++
$ time ./primes < primes.in 2> /dev/null
36
real 0m1.233s
user 0m1.230s
sys 0m0.003s











Топчик
Клёво! Хотелось бы ещё померить, насколько это быстрее: взятие по модулю, конечно, очень дорогая операция, но её обход требует многих других лёгких операций плюс деление.
Я проверял на поиске простых чисел в районе 1095, получилось примерно следующее:
Но всё ещё интересно, как это сработает на числах другого порядка или с другой реализацией длинной арифметики.
Здорово! Со вторым определением N' всё понятно. Но только, кажется, эти два определения не эквивалентны: из первой формулы получается N^(-1) % R, а из второй (-N^(-1)) % R. Нет?
Упс. И правда.
Википедия и прочие слегка к другой формуле расширенный gcd приводят: R × R' - N × N' = 1.
Автокомментарий: текст был обновлен пользователем burunduk3 (предыдущая версия, новая версия, сравнить).
Исправил формулу для расширенного алгоритма Евклида.
А с Barrett reduction не сравнивал? Говорят, может быть ещё быстрее.
Нет. Вообще первый раз слышу про такое, как ни странно.
Впрочем, похожие идеи у меня возникали, когда я пытался разобраться по Кнуту, как быстро делать длинное деление: явно же, что вычислить 1 / n с нужной точностью надо всего один раз, а дальше пользоваться.