Hi all,
The second contest of the 2017-2018 USACO season will be running from Friday, January 19th to Monday, January 22nd.
Please wait until the contest is over for everyone before discussing problems here.
Update: The contest is now live!
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3857 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3463 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 165 |
| 2 | -is-this-fft- | 161 |
| 3 | Qingyu | 160 |
| 4 | Dominater069 | 158 |
| 5 | atcoder_official | 157 |
| 6 | adamant | 155 |
| 7 | Um_nik | 151 |
| 8 | djm03178 | 150 |
| 8 | luogu_official | 150 |
| 10 | awoo | 148 |
Hi all,
The second contest of the 2017-2018 USACO season will be running from Friday, January 19th to Monday, January 22nd.
Please wait until the contest is over for everyone before discussing problems here.
Update: The contest is now live!
| Name |
|---|



Auto comment: topic has been updated by xiaowuc1 (previous revision, new revision, compare).
The contest should be over by now. Can anyone else confirm?
Confirmed. "[...] as you start during the larger contest window starting the morning of Jan 19 and ending Jan 22 at 23:59 UTC-12 time" (see contest rules). Adding 4 hours, all contestants are done at 4:00 UTC-12. Now, it's 5:25 UTC-12.
How to solve gold 3?
First, notice that a string is good if and only if it has a substring consisting of K equal symbols. (That substring corresponds to the last stamp.)
I found it easier to compute the complement — the number of strings where no symbol appears more than K-1 times in a row. You can do that by finding some linear recurrences and then doing an O(N) dp.
Can you elaborate?
EDIT: I deduced a recurrence (see below) and will test it when USACO analysis mode opens. Thanks for the hint. Still interested in other approaches.
f(n) = (M-1)(f(n-1)+f(n-2)+f(n-3)+...+f(n-(k-1))
I found this pattern by working out a 2D DP table on paper, and I had also seen this problem prior to this contest for the two color case.
Here's another idea. Imagine an abitrary string s of length n with < k equal symbols in row (call s good). If we append a symbol x, there are two cases:
s ends with < k - 1 equal symbols or with k - 1 equal symbols and last symbol of s is different from x. In this case, new string remains good.
s ends with k - 1 equal symbols and last symbol is equal to x. Cut the last k symbols from s. We get a good string with n - k + 1 symbols. There are f(n - k + 1) such strings.
Thus, there are f(n) = M·f(n - 1) - f(n - k + 1) good strings.
How to solve plat 2?
Compress the edges.
How can we prove this works? It seems like still O(n^2) worst case?
Can you construct a test case to make it even close to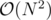 ? I tried but the worst I could get was something like
? I tried but the worst I could get was something like 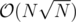 .
.
Compress edges + dfs is still O(N^2) in worst case Consider the following test case
cout<<70000<<endl;
for(int i=2;i<70000;i+=3){
}
good point.
Have you tried this in contest and got AC or are you just saying that you think that this would work?
I came up with a weird solution out of contest that uses a Merge Sort Tree and BITs.
I got AC with it during contest yeah.
What does “compress the edges” mean? Could you point me to some kind of tutorial on this?
Compressing the edges means turning all nodes of degree 2 into a single edge with a larger weight.
For example A--B--C--D with each edge of length 1 might get compressed into A--D with length 4.
Regarding tutorial, sorry I don't know any.
I came up with an O(nlogn) solution during the contest. (I'm not really sure about it though...)
First, let's talk about the obvious O(n2) solution. We just have to run a simple DFS in the tree with every root from 1 to n. Assume that the current root is r, let dep[u] be the depth of node u and mindist[u] be the minimum distance between a leaf in the subtree of u and u. Then we go down from the root and whenever we find a node u such that dep[u] ≥ mindist[u] we stop going down and continue the DFS progress with other nodes. Here for simplicity, let's say that "u is an optimal node for r".
Now, I will demonstrate my idea to optimize the above solution. We will find the result for node 1 first. Keep all optimal nodes for the subtree of u in an array
save[u]. Suppose that we are currently located in node v, and its children are u1, u2, ... Then the candidates of the optimal nodes for v can be all nodes insave[u1], save[u2], ...and their direct parents. Obviously, we should choose the nodes greedily with the increasing order of the distance to node v. We can use some kind of STL likesetto solve this. You may think that this is slow but there is a useful observation: a node can be an optimal node for at most 2 other nodes.By doing that, we can easily compute the answer for node 1. To compute the answers for 2, 3, ..., n, when we run
dfs(u, p)(u is the current node, p is the direct parent of the current node) we should savepair<int,int>(u, p)in a map. If we revisit the statedfs(u, p)we do not go down any further, instead, use thesave[]array that we just find before. Since an edge (u, v) can be visited in two directions: (u, v) and (v, u), so this DFS progress should run approximately 2n times, I guess.This requires a very complicated and tricky implementation. Also, I am not sure whether the solution runs in O(nlogn) because my solution is very slow in practice. If there are any counterarguments, please comment.
My code: https://pastebin.com/J2FmK10Y
Looks like node could be optimal for more than two other nodes. Consider star graph with attached paths of length 1 and 2. Central node of this graph will be optimal for central node of all attached paths length 2. But statement "Total number of optimal nodes for all vertices is linear" still could be correct.
Yeah, you are right... My observation is wrong. My solution cannot pass the "star graph" test case.
I solved it in NlogN starting from the same N^2. With a couple of easy algebraic observations, I deduced a more exact way of seeing the properties that uniquely define those nodes u, and coded a nasty centroid decomposition. I don't understand the time limit/N limit. Most likely the author wasn't able to solve it in NlogN
It sounds very interesting. Can you please explain your solution in more details?
I had the same idea (centroid decomposition) but had to stop halfway during the contest, so I wasn't able to finish it. I don't think the approach is 'nasty' and actually quite like it.
The basic idea is to think of all paths starting in a node. We should count the number of paths where d[u]>=mindist[u] ONLY for the last node on the path (where d[u] is the distance to our starting node and mindist[u] is the minimum distance to a leaf).
With the centroid decomposition in a single step we consider only the paths going through the centroid. Now a path from u to v (not in the same subtree) should be counted for u iff 1) dep[u]+dep[v]>=mindist[v], 2) for all nodes on the path from u to the root dep[u]-dep[x]<mindist[x] and 3) for all nodes on the path from v to the root dep[u]+dep[x]<mindist[x]. The middle can be rewritten as dep[u]<dep[x]+mindist[x] for any proper ancestor of u and the first and last as mindist[v]-dep[v]<=dep[u]<min(mindist[x]-dep[x] where x is a proper ancestor of v). With one dfs we can precompute the ranges of depths for which a certain v can be counted and with another dfs update the answer for that subtree (first removing the subtree from the depths to be counted and re-adding it afterwards).
It seems a 'merge-small-to-large' kind of approach should also work, but (substantially) more difficult to code: Paths from one light subtree to another light subtree can be handled similarly as above. For paths from a light subtree to a heavy subtree we should do some preprocessing before going into the large subtree. For paths from a heavy subtree to a light subtree we should end the processing of a subtree with some information about the depth-ranges in it, so we can do some postprocessing after going into the large substree to handle these paths. In the end it should be possible to do all computations visiting the heavy subtree only once, so also resulting in an NlogN runtime.
Yes, the idea was the exact same one. The approach itself is not "nasty". I was talking more about the code (specifically, my code, which was not the happiest implementation). But you're right, I may have exaggerated. Also, I'm not really sure I understood how you handle the middle condition. What I did was to prove that you don't need to make sure dep[i] > dep[x] + mindist[x] for any ancestor, but rather only for the immediate father, which significantly eases the solution.
I'm not sure which part you don't understand. Maybe my code clarifies things:
I solved it with O((sum of answers) * log N). I think it is O(NlogNsqrt(N)), but I couldn't prove it.
Considering a star graph, insert one vertex into each edge.
The sum of answer will be O(|V|2)
Who know any easy solution for plat 1? Have idea how solve it by maintaining k queues and calculate n·k dynamics using them, but this looks hard to code for me.
Use dp, with state dp[interval][skipped], the brute force transition will be another k factor, but it turns out that you only need to consider one transition (from the leftmost interval that intersects the current interval).
I have an easy DP (I was to lazy to do the contest but it should work).
If there is an interval that covers another one fully, remove the smaller one and decrease K (obviously there is no point in saving a small interval, if we can save a larger).
After this process sort all intervals that are left by r in increasing order. For every pair i < j these inequalities will hold: li < lj and ri < rj.
We start iterating the intervals in increasing order of their r or l. Now consider the following DP:
dp[current interval][number of removed intervals][0/1 flag showing if we have chosen interval i] = answer if we consider all intervals until "current interval" (including it).
We can easily compute dp[i][j][0] - it's simply equal to max(dp[i - 1][j - 1][1], dp[i - 1][j - 1][0]). Now the dp[i][j][1] we will use a small observation: If we chose (not remove) interval x
and let the interval y be the leftmost interval with ry ≥ lx. We can safely remove all intervals in the range [y + 1;x] as they will simply won't change the answer. And the more intervals we remove from there, the less the answer will be.From this we get that dp[i][j][1] = max(dp[p][j — (i — p)][0], dp[p][j — (i — p)][1]), where p is the leftmost interval with rp ≥ li, because it's enough to consider only two case — we either will get the previous interval or won't.
The complexity will obviously be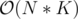 .
.
PS: Maybe some minor details like (+1 or -1 in the DP states) are wrong in the explanation as I haven't checked it, but I think one can get the general idea from reading this.
Exactly what I did! Except I switched dp[i][j][0] and dp[i][j][1].
Passed all test cases during the contest.
I only looked at dp[i-1] instead of dp[p]. Still somehow got AC :D
@Svlad_Cjelli @radoslav11
How can one efficiently save the previous DP states for p when calculating dp[i][j][1] (assuming NK memory MLEs on USACO servers)?
My Code Without Memory Optimization (Also Need Help to Fix WAs on Cases #2 and #3)
NK memory was completely fine for me.
Is it possible to apply wqs on this task to solve K <= 100000 as well? (Something like, let the score for a set S of lifeguards fired be [amount we can cover + X * len(S)], and then binary search on X)?
I'm not sure if this would work, since the cost function here is linear rather than quadratic.
I used convex hull optimization. I think that is what zeliboba was thinking of. Still only O(NK)
How do you use convex hull trick here? The cost function doesn't look anything like a product, right?
It’s increasing and that’s what matters My code
Wait how does this work? Doesn't convex hull trick help you find min/max among a set of lines? Or is this something else?
Convex hull trick helps you maintain the set of dp states that will be helpful at some point in a way that the best past dp state is easily found. I'm talking about the one in this video: here
This isn't a convex hull optimization, but I do think it uses it (dp[n] = dp[i] + smth * (n-i) type) but if it should work I think it will be something like N log N (maybe some more logs)
Yes, it can be solved in NlogN. I don't know how to prove it, but it works (using alien's trick)
I tried to solve it using alien's trick but something is not working and I can't find out what (it works on 6 tests cases out of 10). Can someone please help me?
Haven't looked at the DP but how are you sure that the "cost" in the aliens trick will be an integer?
I was thinking about this but if I used doubles then the answer wouldn't be accurate. Also I remember that we could use integer cost in this problem: https://csacademy.com/contest/archive/task/or-problem/statement/
Weird. For the CS Academy problem, my solution passed during the contest but now by making the costs integers it doesn't. Also I don't understand your point of "the answer wouldn't be accurate".
Answer of the problem is integer. Won't answer differ because of rounding (doubles usually have precision problems)?
No, as the answer in the end is something like "DP answer" + cost * K. You know that "DP answer" is "integer — cost * K", so the end result will be really close to a integer. I get the final answer by doing rounding down of ("DP answer" + cost * K + 0.5) as you can be confident that the double precision error is less than 0.5.
Aha ok, thank you. I will change that.
I changed cost from long long to long double, but now the answer differs even more (I guess because now all dp values are long doubles). Can you please tell me what I need to change so it will work.
plat 3?
I need this one too
There are 2 realizations: 1. The area being water/fertilized will always be one big region 2. The only possible way for a rectangular region to be both water and fertilized is for one sprinkler to be on the SW corner and the other one on the NE corner.
I used 2 arrays to keep track of the running minimum and maximum of the region. I also kept track of the corner/critical points (only the max) (there are redundant points that take up time to calculate). Instead of cycling through all the points for every point which takes O(N^2), I only cycle through the critical points and skip the irrelevant maxs.
In the end, I had to subtract the region that was calculated twice. My AC code
I don't think it has to be one big region — for example you could have sprinklers at (0,4), (2,6), (4,0), (6,2).
But it probably doesn't make a difference for the algorithm.
Here is my O(N) solution. It is similar to xaz3109's solution, but I used prefix sums and some math to speed things up: link
Can you help me find a solution for Gold 2?
Root the tree at Bessie's start and use DP to compute number of farmers for each subtree. Utilize the distance to nearest leaf and compare with distance from Bessie's start. Does this hint suffice?
So, the state for the DP will only include the node? Don't you have to also include distance from the root, which will inevitably run out of time and memory.
Actually, I don't think is DP. It is just a bfs traverse from Bessie's start. So, before, you should have precalculated the distance to closest leaf for each node. In the bfs, each time you arrive at a node which minimal distance from any leaf is lower than Bessie's start, you count one to answer and don't push neighbors in the queue (cause you put the farmer in that leaf and for sure Bessie can't go further).
It makes a lot of sense actually. To precalculate the distance from any node to its closest leaf I assume it's just a BFS from each leaf, but this would be N BFSs at worst. Any hint for this precalculation?
Yes, Since only you care is the minimal distance from a leaf, you can do a multisource bfs. So first push all leafs to queue with distance 0, and then just do normal bfs.
You could also observe that the number of nodes each farmer will move up is floor(depth/2), if you root the tree at Bessie's start. Then use binary lifting to efficiently calculate the kth ancestor of each leaf.
OK. In fact, I solved it using DP. Let dp[i] denote the minimum number of farmers required for the subtree rooted at vertex i. If the distance from start to i is ≥ distance to nearest leaf from i, we have dp[i] = 1. Else, we have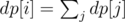 where sum is taken over all children of i.
where sum is taken over all children of i.
I did a greedy solution, maybe over complicated it.
Lets make a DS, that can solve these queries -
1. Activate a node.
2. Find minimum distance to an active node from a given query node.
It can be done with Centroid Tree.
Now, in our problem, lets sort the leafs according to their distance from Bessie. Call them v0, v1, ..., vk - 1. Now pseudo code is something like this —
Exactly same with Gold 1: http://www.spoj.com/problems/ADABRANC/
By the way, how to solve Gold 3? Tried dp with inclusion-exclusion, but seems it was not enough to find solution.
Start reading here. :)
Hi there, I'm the problem-writer behind Gold 1 :)
First of all, I hadn't seen this problem before writing my problem. However, because USACO Silver and Gold use very limited subsets of the material tested in programming contests, it's natural that problems will use similar ideas over time. Indeed, after I wrote the problem (but before the USACO contest), a problem on a CF round reused an extremely similar idea: http://codeforces.net/contest/915/problem/F
The similarity between these two problems is not quite so uncanny, but anyone who had solved both would surely notice that they rely on the same idea.
Moreover, it's worth noting that anyone who has studied the Silver and Gold-level material so thoroughly as to be able to find this type of thing on short notice probably is ready for promotion anyway. Any contestant who had somehow already seen this problem almost certainly did so in the process of solving a far greater number of relevant problems, in which case they'd most likely achieve promotion regardless.
My apologies for the similarity--however, as we've seen here, it is extremely difficult to create ideas that nobody has ever come up with before when we're able to use such a small subset of the contest material. Situations like this should definitely be avoided in Platinum, but for the lower divisions, they're very likely to show up simply because almost all elementary ideas have been discovered already.
Of course, it is really hard to came up with new problem with unused idea. I wrote above comment without any offense :)
None taken! I just wanted to clarify, especially to make it clear that the problem was not written directly as a copy of the one you linked. :)
Noam527 solved it with combi (not sure if PIE), maybe you can pm him
I didn't, I just thought it was with combinatorics before I solved it.
How do you do Gold 1?
Sort the queries by threshold and use DSU to update tree. Since number of vertices is required to be reported, store size of each set/component and union-by-size will give you AC.
Any prediction of gold-to-platinum promotion cutoff?
I've looked and in the past years for January it seems to be 700 or below.
(Personally) I found the gold contest quite lenient on the partial credit, as I was able to get about 70% for #1 and #2 without really understanding the correct solution (probably ~700-720 total). For #3 I did an N^2 dp instead of the correct O(N) and only got the first 9/12, as I imagine many others did as well So I'm worried a relatively high amount of partial credit awarded might make the cutoff 750 or above,
Anyone else have any thoughts on the relative difficulty? This is only second gold contest for me so I'm still new
For G1 I got 9/10 with suboptimal solution :)
Does anyone know how to compute continuous intervals for S1?
Make an array len[] which len[i] means how many units of i'th interval will remain from intersections to other intervals if delete i'th inverval. For calculating len[], sort intervals by R and update len[i] like sweep line. Rest is easy.
I tried to download the test cases for plat 2 but when I open test case #2, a string of seemingly random characters in a variety of languages appears. Anyone have a solution to this?
What are you using to open it? Notepad is what I use and it works perfectly fine on that.
Try using atom, it will open them up all in one place too.
There is a problem with author's solution in Gold 3.
cout << (((long long)ans) + MOD — ((long long)s[N]) + s[N-1])%MOD << '\n';
should be
cout << (((long long)ans) + MOD — ((long long)s[N]) — s[N-1])%MOD << '\n';
I believe the solution is correct as is, though the number of parentheses is admittedly confusing. We are subtracting s[N] - s[N - 1] from the total number of ways.
I came up with a nice solution for Plat #2 that runs in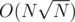 worst-case time. It takes 350ms on the test cases from the contest.
worst-case time. It takes 350ms on the test cases from the contest.
Let dp[n][k] be the number of farmers needed to stop Bessie when she is starting from node n and only allowed to visit nodes in the n-subtree, after the farmers get a head start of k time steps. Similarly, let dp2[n][k] be the number of farmers needed to stop Bessie starting from node n with a k time step head start for the farmers, but Bessie is only allowed to visit nodes not in the n-subtree.
First, set dp[n][k] = dp2[n][k] = 1 if n is distance at most k from a leaf. You can then proceed to make the following observations about state transitions.
The answer for each node is either 1 if it is a leaf, or dp[n][0] + dp2[n][0]. We thus have a solution for the problem in O(N2) time.
To improve our algorithm to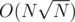 , note the following key lemma:
, note the following key lemma:
Lemma: For any fixed value of n and varying value of k, both dp[n][k] and dp2[n][k] take at most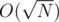 different values.
different values.
Proof (by pacu): Giving a head start of k is equivalent to removing all the leaves from the tree k times. The value of dp is limited by how many leaves in the tree there are. Thus, supposing there are at least x different values of dp, the number of nodes in the tree must be at least 1 + 2 + ... + x = O(x2), which completes the proof.
We can thus use a variable-sized vector of distinct values and indices for each node instead of an array, updating state transitions with the merge operation from mergesort. This gives us a solution using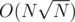 time and memory.
time and memory.