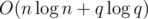instead of set you can use vector of pair and do binary search over it.

Maintain a data structure (eg. Segment Tree) which do the following: for each L-index, store the maximum R-index that match (go in pair) with it. Then when you need to find set containing x, you just need to get Query Max R-Value of all L-index that <= x. If the data is way too big (1e9 or 1e18), you can use discretization

Assuming you have multiple queries that you can do offline and you only need to find any pair in which x is present not all pairs I would do the following.

Sort the pairs by their left endpoint and if two pairs have the same left endpoint put the one with a larger right endpoint first. Then I would construct a new vector of pairs. First put a pointer at the start and set r to the right value of the first pair in the vector. Then move the pointer forward if we find an interval with a right endpoint greater than r update r and add it to the new vector otherwise ignore it.

Next take all the queries sort them and put the pointer at the start of our new vector of pairs. If a value is in the interval pointed to by the pointer this interval is our answer for the query. Otherwise move the pointer forward until we find an interval that works. Then move on to the next query. Finally put the queries back in the original order and output the answers.

Complexity assuming q queries and n pairs will be for sorting the pairs. O(n) to construct the new vector. 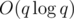to sort the queries. O(n + q) to answer the queries. O(q) to put the queries back in the original order (we can use counting sort). Final complexity