Блог пользователя legendjohn9999

How to find the diameter of a graph, which have only one cycle(N vertexes, N paths)?
Автор legendjohn9999, история, 7 лет назад, По-английски

Hi All. Is there any LINEAR algorithm to find the diameter of a graph, which have only one cycle(N vertexes, N paths)?

  • Проголосовать: нравится
  • +11
  • Проголосовать: не нравится

»
7 лет назад, # |
  Проголосовать: нравится +21 Проголосовать: не нравится

How do you define the diameter? Maximum shortest path between two vertices or simply the longest simple path in the graph?

For both ways you divide the problem into two parts. The first path is to erase the cycle and for every tree in the resulting forest to find the diameter.

Now in the second part we should only consider vertices from different trees in the forest. Obviously for every tree it will be optimal to choose the vertex with largest depth. Well we choose these vertices and now the problem is transferred to a cyclic array. This simpler problem can be solved with segment tree in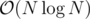 . is also possible if we simply keep one variable instead of the tree.

→ Ответить
  • »
    »
    7 лет назад, # ^ |
      Проголосовать: нравится 0 Проголосовать: не нравится

    Thank you for answer! I was about maximum shortest path between two vertexes. I understood the first part of yours solution, but I cant undetstand how you solve the problem with segment tree, before choosing vertexes with largest depth, from all components? Can you please eleborate your solution more deeply?

    → Ответить
    • »
      »
      »
      7 лет назад, # ^ |
      ← Rev. 2   Проголосовать: нравится +8 Проголосовать: не нравится

      The idea is:

      You get the vertices in the cycle. They form a cyclic array. Now let's denote by di the largest depth to the tree linked to the node at position i in the cyclic array. If the there is no linked tree, di = 0. If there is more than one linked tree — we chose the maximum of their depths. Now the problem becomes:

      Given an array d of size s, find the largest value of min(|i - j|, s - |i - j|) + di + dj, for any i, j, such that i ≠ j.

      We will solve this by duplicating our array and placing it after itself. This way we will have a new array a of size 2 * s.

      Now note that min(|i - j|, s - |i - j|) = i - j, if we have that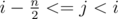 . Well now if for every i in the array a we consider only such positions j and we find the maximum, we will have the the answer to the problem.

      Well now we have to find for every position i the maximum value of i - j + di + dj, where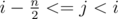 . We will group i - j + di + dj like (i + di) + (dj - j). Here (i + di) is a constant as it doesn't depend on j. Well now we must find the maximum of (dj - j) in the given range. Ohhh this is the default RMQ problem!

      To get O(N), we can notice that the ranges in which we want the RMQ are of equal length. Here comes the monotonic queue rmq. Here is a blog about it by bicsi (the first part).

      PS: Of course you shouldn't forget to find the diameter in every separate tree when we remove the cycle.

      → Ответить