Given n circles n <= 1000, how can I find the area of union of all this circles?
→ Обратите внимание
До соревнования
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
5 дней
Зарегистрироваться »
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
5 дней
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 25.11.2024 15:31:16 (j2).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











I'm interested in that kind of problem too..! http://www.spoj.pl/problems/VCIRCLES/ is a small version but the big one is http://www.spoj.pl/problems/CIRU/
The main idea here is to make a vertical decomposition: draw a vertical line through every point of two circles' intersection and through two points with maximal and minimal x of every circle. Hence, you'll have O(N^2) vertical bands. In each band you have something like brackets (arcs) sequence so you can skip inner brackets. At last, you have some trapezoids with arc as side edges. Their area can be easily found in many ways.
please describe any of them....
How do you do the "easy" part in less than O(N)? :)
There is a way, I think. But I never implemented it myself. You can try to build planar graph where vertices are points of circles intersections and edges are arcs. Then you can use standard algorithm for finding the area of faces of the planar graph. The only problem is how to sort edges, connected to one vertex. I am not sure about how do it correctly.
are there questions based on area similar to this on CodeForces?
You can try this (not exactly same but similar): https://codeforces.net/contest/814/problem/D
This problem can be solved with Green’s Theorem : Find the arcs which lies in the border of the union of area (in n^2lgn time with sweep), and apply the formula directly.
This can be solved using Green's Theorem, with a complexity of n^2log(n). If you're not familiar with the Green's Theorem and want to know more, here is the video and notes from Khan Academy. But for the sake of our problem, I think my description will be enough. The general equation of Green's Theorem is
If I put L and M such that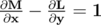
then the RHS is simply the area of the Region R and can be obtained by solving the closed integral or LHS and this is exactly what we're going to do.
So Integrating along the path in the anticlockwise gives us the Area of the region and integrating along the clockwise gives us negative of the Area. So
AreaOfUnion = (Integration along red arcs in anticlockwise direction + Integration along blue arcs in clockwise direction)
But the cool trick is if for each circle if we integrate the arcs which are not inside any other circle we get our required area i.e. we get integration in an anticlockwise direction along all red arcs and integration along all blue arcs along the clockwise direction. JOB DONE!!!
Here is the GitHub link to my C++ Code