Hey!
Tell me plz how to find the diameter of a tree using DP. Thanks in advance! :)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 4 | atcoder_official | 161 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
| Название |
|---|



Use DFS!
Oh, that's not interesting)
that's not dynamic programming. but thanks, anyways.
can you explain in step 3 why have you asked to repeat step 2 , two times. once i have the farthest node from root (lets mark it as A)only one more time DFS(A) should yield another node(let say B) that is farthest from A node and the question seem to be solved. Please correct me if i am wrong.
Yes, one time is enough.
I guess he had meant that you need to do step 2 two times in total.
Another way. Run DFS from the root. In each subtree, we find the length of the longest path from the root of this subtree to some descendant of it. It is clear, how we can compute the answer for some vertex. We solve the problem for each of its children, and the answer for this vertex is 1+max where max is the longest path from one of the children to some descendant of it.
Then the answer to the problem is the maximum value over the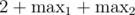 , for each vertex and two of its children.
, for each vertex and two of its children.
Thanks for the idea, but I think it won't work at this test, for example
1 2 2 3 3 4 3 5 3 6
Because 1 has only left subtree
Well, of course, we need to consider also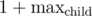 , for the root, if it has only one child. Thanks for the note.
, for the root, if it has only one child. Thanks for the note.
and here comes another question: why do we find the path that covers the root of the subtree. I think that's not true. For example,
1 2
Your answer is 7, but it should be 5. Thanks for the reply.2 3
3 4
2 5
5 6
6 7
1 8
Wait, why 7?
cause dfs(2) = 5, dfs(8)=0 5+1+0+1=7, if I understand you correctly)
No, no, dfs doesn't return that value. Think of it in this way: first we calculate only max values for each of the vertices, and only then we try to find a pair of two children of some vertex which maximizes the 2 + max1 + max2. So, for example, in this case:
why dfs(1) = 4? it should be 5 And dfs(2) should return 5 (4-3-2-5-6-7), shouldn't it?
I counted the number of edges, not the number of vertices on the path.
Yes, but 4-3-2-5-6-7 is the longest path and amount of edges is 5
############################################
Yes, and when we look at vertex 2 (after dfs), we see that child 3 has max1 = 1 edges, and child 5 has max2 = 2 edges. So we can relax our answer to 2+1+2=5 edges.
I finally understood. Thank you!
Great! And I think it can be counted as DP. (:
sorry to disturb you after 7 years, can you tell me how to find end nodes of diameter?
Check the editorial of problem F from Codefoces #615(Div.3)
store the best and second best depths of children of every node in dp[node].
Here's the code for storing all values