Hi all,
The third contest of the 2017-2018 USACO season will be running from Friday, February 23rd to Monday, February 26th. This will be the last contest before the US Open, scheduled for March 23rd to March 26th.
Please wait until the contest is over for everyone before discussing problems here.











Does the difficulty level increase with each contest or will it this one too have the same difficulty level as the previous contests?
About the same. Difficulty increases according to the division.
Dont try it, its so hard for us — green people
The bronze isn't that bad, even for greens.
Also, if you never try, you will never improve.
"Even for greens"???
Bronze is not hard. It is just implementation.
It gets more hard when you advance to the next division.
You dont try. This is the reason why we are green !
Then i think it's best to improve ourselves.
Guys,i don't understand why users dhruvsomani,Flying_Dragon_02,MazzForces get downvotes,they did nothing wrong,it's just their opinions and questions,please stop downvoting them.
Hi, I read participation is open to all. Can someone please help me with the division ( gold silver etc ) participation rules. Can I directly participate in gold / silver , or give multiple divisions in the same contest ?
You start off in bronze. You can get promoted to the next division during the contest if you do 100%, and you'll get promoted to the next division after the contest if you get at least 75% (it can change though, last time it was 60% to go from gold to platinium).
So if you do 100% you can do the silver contest, if you 100% again you can do the gold one and so on...
Thank you
I got to silver already. If i don't do well in silver, will i be demoted to Bronze again?
no
For more information:http://www.usaco.org/index.php?page=instructions
Predictions for Silver Cutoff? I got 700 exactly.
Contest is not over yet.
Sorry
Please don't discuss any part of the contest until it is over. It is not allowed.
The contest should be over. Can anyone confirm?
Thank you very much for an easy #2. :)
Contest is over for everyone.
For those who competed in Platinum:
We can visualize each query as a point (a, b) on the plane, and each slingshot as another point (x, y) with value z. The answer for a query that uses this slingshot is the Manhattan distance between these two points plus z.
For simplicity, let's assume that we only care about queries (a, b) to the top-right of a slingshot (x, y). Our cost, then, is (a - x) + (b - y) + z. However, since we'd like to update many query points, we will leave a and b out of the equations and add them back individually for each query.
If we sweep from left to right, then any query that comes after (so a ≥ x) that satisfies b ≥ y is a candidate to get updated. Essentially, we want to update all values ≥ y with - x - y + z, which we can do using a segment tree (note that instead of 1, 2, 3..., the leaves will be y1, y2, y3...). When our sweep reaches a query point, we simply have to find the value in our segment tree at location b (let's call it m) and update the answer for that point with m + a + b. We repeat this process for the other three quadrants to get our final answers.
We should look at the diameter of the tree when answering queries.
The maximum distance will be the length of the path from our node to one of the endpoints of the tree's diameter.
Our graph is a forest, so let's keep track of each tree separately. For each tree, we will maintain a sparse table which allows us to find the LCA (and distance) for any two nodes. Additionally, we will need to keep track of the endpoints of the tree's diameter.
Now, we must perform two types of operations:
When we add a node, we will calculate its sparse table entry in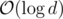 , where d is the depth of the node.
, where d is the depth of the node.
Additionally, adding a node may cause the tree's diameter to change, so we need to update it accordingly.
In the above diagram, A and B are the endpoints of the old diameter, and C is our new node.
When we add node C, the diameter of the tree will either stay the same or become the path from C to an endpoint of the old diameter. We can find the lengths of these paths using our sparse table and update the endpoints accordingly.
The furthest node from a given node will always be one of the two endpoints of the tree's diameter. So, we can just query the distance to the endpoints and print out whichever distance is greater.
Thanks to kamishogun for explaining this one to me!
The maximum number of cows on any platform is at most one more than the minimum number of cows on any platform. That is, every platform has either x or x + 1 cows.
The number of ways to arrange cows using x or x + 1 on each platform is the number of ways you can make a sequence of length n using only two distinct digits such that it repeats every x numbers (keep in mind that it's a circle!).
The number of ways you can make a sequence of length n using only two distinct digits such that it repeats every x numbers is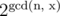 .
.
Since n ≤ 1012, we can't loop over all values of x. Instead, we use the Principle of Inclusion-Exclusion (PIE) to calculate how many numbers y there are such that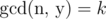 for every k.
for every k.
We need 1 ≤ x < n, but to make the computation easier, we'll consider 1 ≤ x ≤ n and remove the extra case afterwards. We'll use a list of the factors of n in descending order, and at the end, we need to subtract sequences like 2222 and 3333 that got counted twice.
Very nice solution of 2. I was trying to come up with something like this (sparse table + LCA) but I did not notice all the properties of a diameter. I ended up coding offline centroid decomposition...
Every node and a query appear at a different time. You will be answering the query, using values which appeared before that query.
The idea is that for each query, you will be traversing the centroid tree (going up by centroid parents), calculate the distance from the query node to centroid and from centroid to node with max distance, in a different subtree.
In each centroid you store the vector of 2 best pairs(max distance, direct child of a centroid, through which this distance is realized) — second pair must have a different direct child than the best one, for each node in centroid component.
First, you record a distance and a direct child of a centroid, for each node within centroid component (you start dfs from each child of a centroid, calculate distances and remember the root). You record these values under different times as every node has a different arriving time. You have the best pair for each particular time and you sort these values acording to time.
Then you count best and second best pair for each prefix (the best values seen so far). We need that as we will be looking for a max among the nodes which arrived earlier than our query. It means that if we have a worse value at time j than at time i and j > i, we should use value from time i instead.
You answer each query by traversing the whole centroid tree and for each centroid get the max value for max time, which is less than the query time — upper_bound. You just need to check if the direct child of the centroid, which realizes best value, is the parent of the query node. If that is the case, use the second best value, for a different direct child. Also at the beginning you should check that the centroid appeared before the query, if this is not the case, skip it and go to the parent centroid.
Quite an overkill thow, compared to the nice, online solution...
Intended solution is n root n but I didn't notice the better way. This is also better than it...
It was supposed to be batch processing, LCA on the root N in the block for their shortest distances, and then every time the block reaches root N to perform a tree DP to update the distances for each node. But it turns out there are much better solutions.
I have a solution to Slingshot which could possibly be interpreted as simpler than yours.
First of all, let's notice that the slingshot you use for a query, if any, is going to shoot you in the same direction. So we can separately consider left-to-right slingshots and queries and then right-to-left slingshots and queries.
I will explain how to solve the left-to-right case. For the right-to-left one, just swap the x and y values for all queries and slingshots which were right-to-left initially.
Consider some query (X, Y). Regarding the positioning on the number line, we can distinguish 4 cases for the optimal slingshot (A, B, T), if any:
X ≤ A ≤ B ≤ Y. In this case the cost is A - X + T + Y - B = (Y - X) + A + T - B. Since Y - X is constant for a given query, our task is to find the minimize A + T - B among all slingshots satisfying the aforementioned condition.
X ≤ A ≤ Y ≤ B. In this case the cost is A - X + T + B - Y = ( - Y - X) + A + T + B. Since - Y - X is constant for a given query, our task is to find the minimize A + T + B among all slingshots satisfying the aforementioned condition.
A ≤ X ≤ B ≤ Y. In this case the cost is X - A + T + Y - B = (Y + X) - A - B + T. Since Y + X is constant for a given query, our task is to find the minimize - A - B + T among all slingshots satisfying the aforementioned condition.
A ≤ X ≤ Y ≤ B. In this case the cost is X - A + T + B - Y = ( - Y + X) - A + B + T. Since - Y + X is constant for a given query, our task is to find the minimize - A + B + T among all slingshots satisfying the aforementioned condition.
Turns out that we can solve all four cases independently offline with the help of sweep line and segment tree for minimum.
In cases 1 and 2, we sort the queries and slingshots in order of decreasing X or A. Then we loop over all queries while also keeping a pointer of the last slingshot inserted into the segment tree. Whenever the X of the current query becomes less than or equal to the A of the next slingshot to be inserted, we simply update on position B with + A + T - B for case 1 and + A + T + B for case 2. After all updates resulting from the current query are done, we simply try to update the answer of the current query with (Y - X) + minquery(X, Y) in case 1 and with ( - Y - X) + minquery(Y, ∞)) in case 2.
Cases 3 and 4 can be handled in the same way, we just have to sort the queries and slingshots in order of increasing X and A.
The whole code isn't that long if you implement the segment tree structure once and use it for all 4 cases. It was about 200 lines of code for me, also including some long comments before all cases. Unfortunately, I delete all my codes after a contest and I have to wait for the final results before I can access my solution and post it here.
can I ask, why do you delete the code after contest?
Because for contests I have a folder Work and in there I create all A/B/C/... folders and then when the next contest comes, I have to empty the Work folder and create new folders :D Just bad practice, I don't know how I employed it :D
Here is my AC code for Slingshot. It uses the same solution described by P_Nyagolov.
Code.
I heard from bovinophile that problem 1 can also be done with a k-d tree.
PS: I used a 2d segment tree (which is O((N + M)log2N)) to do queries online for #1 but it only got 3/10. Turns out that the brute force O(NM) solution got 5/10. :(
Well this is expected if you do dynamic 2D segment tree instead of the compressed offline one, because the constant in it turns out to be huge.
I agree, but I feel like this should get at least as much credit as brute force. :P
At least you didn't spend 3 hours constant optimizing Nlog^2N for p2 and then thinking about how to remove a logN factor, to no avail.
Guess thats what happens when you make everything a function
Hey that's basically what I did for p1 :P
At least you weren't 5 seconds away from a correct solution to 2. Had two cases, submitted the correct solution without having a print statement, got WA on sample, added print statement, uploaded, just as time ran out...
And the new code gets 9 cases out of 10. Sad life.
sad :(
This is my code for Problem #2 if anyone needs it; it's pretty short and simple. My solution was inspired by this problem that I encountered before. Thanks to Aviously for giving me credit for the solution.
I also remembered that problem but I did not notice hint 2 (in the post above) and wrote that whole centroid stuff. I am a little angry as it would have taken me 5 minutes to change that solution, instead of 2 hours to implement and 1 hour to debug the new approach...
At least got some centroid practice :)
When adding a node and the diameter changes, why must one of the endpoints be one of the old diameter's endpoints?
You can use well know fact (or prove it on the paper) that if you have node x, go to the farthest node y, then go to the farthest node from y, z. y-z is a diameter.
Now you have d1-d2 (diameter) and you add x. Let's assume that for parent[x], d1 was the farthest (based on the property above). Then for x also d1 is the farthest. For d1 so far d2 was the farthest and now it could be changed only to x. If that's the case, we have a new diameter.
Notice that when you add a leaf u as child of a parent p the distance between all other pairs of vertices remains constant.
This means that the new diameter must either be the previous diameter v - w or be u - x for some vertex x. Suppose it was u - x. Then x must be the farthest vertex from u. But the farthest vertex from u is obviously the farthest vertex from p, which must be v or w. So thus the resulting diameter after adding u is either v - w, w - u, or u - v. Thus, when processing an add query, you can just check these three cases (using lca or whatever) in O(logn) in order to determine which of them it actually is.
Silver 3? I'm pretty sure it had something to do with medians- sort of like a 1d minimum sum of distances problem with a twist.
No, it's a ternary search.
If anyone needs codes for the Platinum problems, here are my accepted solutions. I think they are the same as the ones in Aviously's comment, but I'm not sure as I haven't read his whole comment.
https://ideone.com/xlpNy6
https://ideone.com/tfVpDY
https://ideone.com/wMsA7P
In problem 2, your solution is offline, whilst Aviously's solution is online. You don't need to read everything first, to build LCA structure.
Edit. I like that feeling when I barely manage to solve one task during the contest and later I discover that everybody here is getting max score :) Congrats!
Results are out!! http://www.usaco.org/index.php?page=feb18results
I have a problem. Code I submitted for Platinum 1 gets 1/10 at competition site. But if I download test cases and run them locally one by one, all of them are correct. When I run all them with my grader, the same problem occurs as at competition site (results are large negative numbers). Can please someone explain why this happens and how can it be avoided?
Disparities between your computer and the grader, perhaps. Try running your code with warnings, checking for uninitialized variables, etc.
I'm just curious, does anyone know how they determine the order to list participants with the same score: by time spent, random, or something else?
It's random-- I believe I actually emailed Brian Dean once, out of curiosity.
The test data for Platinum problem 1 is too weak... If you sort all the slingshots and for each query, use the nearest 3400 slingshots to update the answer, you can pass all the tests.
This strategy helped me to score full points.
total 1700 slingshots also adequate for answer :)