Auto comment: topic has been updated by vintage_Vlad_Makeev (previous revision, new revision, compare).

Auto comment: topic has been updated by vintage_Vlad_Makeev (previous revision, new revision, compare).

Auto comment: topic has been updated by vintage_Vlad_Makeev (previous revision, new revision, compare).

"BONUS (medium): Given graph is not properly colored, but you don't have to minimize size of the set. Can you solve it?"

Yes, that's what I solved yesterday before solving actual problem xD

"BONUS (hard): Find answer minimizing number of subsequences."

Sorry if I'm missing something but isn't number of subsequences always equal to number of 0s — number of 1s, as each subsequence chosen increases number of 0s — number of 1s by 1.

The two bonuses for "Binary cards" are the same, should they be?

Please help in ques C, why am i getting TLE

http://codeforces.net/contest/950/submission/36191394

Thanks

"BONUS (medium): Given graph is not properly colored, but you don't have to minimize size of the set. Can you solve it?"

If a person stores his data at computers x and y and initially color_x = color_y then if x is in the set we choose then y won't. Similarly if y is in the set then x won't. This is NAND 2-Sat clause. Additionally like in the statement we add directed edges for the cases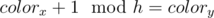 — they are equivalent to implications.

Well now for the medium problem we simply need to find a valid 2-SAT solution with at least 1 variable true.

Well we simply try fixing all possible variables to be true and then check for a solution. This way we achieve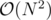 . Probably there is a faster way to do it but still this should work.

The main reason for this comment is because I think I have a solution for the hard version. Not sure it's correct tho.

So let's assign costs to the vertices. We assign a cost of -1 to all variables x and a cost of 0 to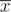 . Now we search for a 2-SAT solution of the maximum cost with at least on 1 set to the original variables. Well this should be possible to be solved with the Maximum closure algorithm.

We again try fixing every variable and then running the algorithm.

The overall complexity will be .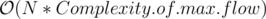

UPDATE: it's wrong.

Can anyone tell me how to maintain the list of zero's and almost zero's efficiently in the problem 949A-Zebras?

In F, what's the exact expected number of intersections we need to check, without O-notation? I solved the problem with a different random scheme, but had to const-optimise like crazy to be able to compute a sufficient number of intersection points. Since (2N)² is approximately 27 million and computing one intersection + checking if it's valid requires a lot of operations, that 5s time limit is really tight. Even worse, with a non-deterministic solution, there's a non-zero chance of any solution having to check twice as many intersections on some test and getting TLE there.

I'm not surprised it has so few successful solutions to date and the only 2 solutions that passed pretests failed systests. Designing a solution that passes systests through anything but luck seems impossible (unless it's deterministic — does such a solution exist?).

It seems I have a solution for E that's linear in N and almost independent on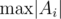 (just through polylog).

The extra observation is that when we decide to use cards for the first k bits and skip the card for bit k + 1, we can shift each A_i by any number in a common fixed range [l, l + 2^k) that contains 0 — the value of l can be chosen arbitrarily by setting the cards' signs. This shift needs to make each A_i divisible by 2^k + 1, but since we can only shift by at most 2^k - 1, the number we need to shift to is uniquely determined. This tells us a possible value of l for a given k (or that it doesn't exist).

This gives an obvious recursive, possibly exponential solution: try all possible k, shift each A_i and divide by 2^k + 1, solve for this modified array recursively if it's possible to choose a valid l (stopping when everything is 0) and add k cards; choose the option that gives the fewest cards.

Now, intuition says we could take the first k that gives a valid l and set of shifts. I don't have proof this works, but I submitted it and got AC. (In fact, I got AC even with the possibly exponential solution. Idk if it can be hacked or the tests aren't strong enough?) Either way, since the recursion doesn't fork, this is clearly .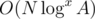

It seems there is a typo in the solution of 949B — A Leapfrog in the array. It should be "At the moment of jumping to cell p there are p/2 elements to the left of the position p". Please correct me if I am wrong.

Sorry for the necropost, but I think someone needs to .......do something about editorial of Div 1B. Anyways, there is a mistake in the editorial( as mentioned in one of the comments above) . For an even position P, there are P/2 elements to the left (and not right) of it. Thus there are n-P/2 elements to the right of position P. Now, we can say the element at position P+(n-P/2) would have jumped to position P. We can observe that the answer for an odd P is (P+1)/2. So,we just create a while loop, and for each iteration, set P = P+(n-P/2) . When P becomes odd, output (P+1)/2 and break the loop. Make sure to take care of overflows. The overall complexity is log(P) per query. I wanted to see if the editorial mentions a constant time solution, I think there should be one possible. But damn, this editorial for problem 1B was confusing.