I am recently solving a problem to find a^(n!)%m and got stuck. please suggest how to solve this problem and some resources and problems to learn concepts related to modular arithmatic.
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 157 |
| 6 | Qingyu | 156 |
| 7 | adamant | 151 |
| 7 | djm03178 | 151 |
| 7 | luogu_official | 151 |
| 10 | awoo | 146 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Feb/23/2025 22:36:13 (i1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











What are the constraints for a, n, and m?
If a and n are small, and gcd(a, m) = 1 (a & m are coprime)
Then first, remember that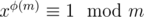 where φ(m) is the euler totient function of m. That means, we can simplify
where φ(m) is the euler totient function of m. That means, we can simplify 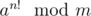 to
to 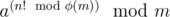
You can calculate φ(m) in O(sqrt(m)) and then calculate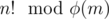 in O(n) and then the power with binary exponentiation in O(log2(m)) so the total complexity is O(sqrt(m) + n + log2(m))
in O(n) and then the power with binary exponentiation in O(log2(m)) so the total complexity is O(sqrt(m) + n + log2(m))