На этой неделе (26-30.03.2018) проходит республиканская олимпиада в г. Минске. Как обычно будет два тура, на которых будет предположительно по 4 задачи. К сожалению задачи будут, наверное, сильно сложными для меня, поэтому предлагаю обсудить решения в комментариях к этому посту. А можно обсудить не только задачи :)
Желаю удачи всем участвующим школьникам!
Первый тур
Задача 1. Галактика
Условие
Решение
Чтобы решить исходную задачу, необходимо решить три более простые задачи для каждой отдельной координаты.
Решим задачу для координаты X.
Пусть мы выбрали x, тогда ответ будет равен: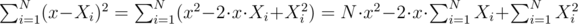 
. Предподсчитав 
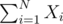и 
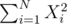, можно за O(1) перебрать все координаты.
Сложность по времени: O(N + M), по памяти: O(1).
Бонус: попробуйте решить задачу для M ≤ 109 за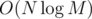 
. К сожалению придется использовать __int128, но самое интересное — это идея, а не детали реализации.
Задача 2. Поиск в перестановке
Условие
Решение
Можно получить легкие баллы воспользовавшись std::nth_element(). К сожалению, у данного алгоритма константа количества сравнений точно больше 
, поэтому полные баллы не удастся получить, но 90 баллов — запросто.
Задача 3. Спортивная трасса
Условие
Решение
{{ Решение задачи }}
Задача 4. Дерево удачи
Условие
Решение
{{ Решение задачи }}
Второй тур
Задача 1. Несложная задача
Условие
Решение
{{ Решение задачи }}
Задача 2. Город художников
Условие
Решение
{{ Решение задачи }}
Задача 3. Реорганизация
Условие
Решение
{{ Решение задачи }}
Задача 4. Лабиринт
Условие
Решение
{{ Решение задачи }}
КУ
КУ
КУ
КУ
КУ
КУ
КУ
КУ
КУ
КУ
КУ
Depth = 9, OK UPD: Я не знал, что максимальная глубина = 9, почему нельзя было реализовать это рекурсивно?
скоро ли появятся условия ?
Скоро
В первой задаче нужно же всегда смотреть на среднее значение. Или на две точки, если среднее получается не целым, доказывается взятием производной.
1_2(100): За (n-1) запросов к библиотеке можно построить дерево отрезков, в каждой вершине которого будем хранить позицию минимального элемента в массиве на этом отрезке. Далее (k-1) раз за (log n) запросов удаляем минимум. Позиция k-ого минимума как раз и будет ответом. Итого запросов к библиотеке n-1+(k-1) log n.
Пробовал кто-то это реализовать? Выглядит как O(2·N) операций сравнения, что плохо наверное.
UPD. Ух как заминусовали. Сразу видно, что я слишком слаб, чтобы понимать такие сложные структуры.
Я на туре написал на 100. Мы же вызываем IsLess только при объединении двух сыновей, поэтому при построении мы делаем ровно (n-1) запросов к библиотеке.
Код на с++
Условия второго дня