I have code of finding the perpendicular distance from a point to a 3D plane. But in this case, the plane is infinite. If the plane is not infinite, but limited to a certain piece, such as the face of an object, then how to find the minimum distance from a point to that face?
An example:
If the 3 points defining a "piece" of plane are:
1 0 0
0 1 0
0 0 0
And the query point is:
1 1 1
Then the answer will be 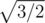 .
.
Is there any implementation in C++ for this problem? If yes, then could someone please provide it? And if not, then sharing the idea of solving it will also help. Thanks in advance.










Let h be the distance from query point Q to the plane Π that contains the face. Project Q onto Π, then find the distance d from this projection to the face (this becomes a 2D problem). Your answer is then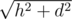 .
.
And when I say "this becomes a 2D problem" I mean actually make 2D points: if you have two perpendicular unit vectors v and w in Π then you can find the 2D coordinates of some point P by computing (P·v, P·w).
For the code you would need something like this (details to come in my book once I've written that part):
Use
distfor h and then usepos2don all the points (including Q) to make the problem 2D and compute d.Did you stop working on your geometry book?
No, I'm still working on it, it's just taking much more time than I anticipated (especially all the darn figures). I made some progress lately, and I will post an update in a few days. :)