redocyz's blog

Google Code Jam Round 1B
By redocyz, history, 7 years ago, In English

Just a reminder that Code Jam Round 1B starts in under 24 hours.

Let's discuss the problems here after the contest.

  • Vote: I like it
  • +89
  • Vote: I do not like it

»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

reminder: 55 mins

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

If we qualified off the first round, is it possible for us to submit solutions to the second round without appearing on the scoreboard during the competition?

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Hey, how can I see the test cases for the visible test cases? I made a submission and my submission simply says "Wrong Answer". I remember previously we could see test data of the small set.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Now it isn't possible to see test data other than the samples.

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I am getting WA in the 2nd Problem.

My idea is binary searching on the length.

To figure out if length L is ok or not, I will move with a sliding window maintaining number of Lefts, Rights, Pairs(Left,Right), for a window starting at index i, I will count the number of Left[i] + Right[i] + Pairs(Left[i],Right[i]) or Left[i] + Right[first Index to the right of i which has a different left] + Pairs(Left[i],Right[first Index to the right of i which has a different left]) and the same for the first index to the right of i which has a different right. if any of those numbers are equal to m then I can have an answer of m or may be more.

What is wrong here?

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How to solve the last task?

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it +5 Vote: I do not like it

    Read the analysis.

    For test sets 2 and 3 I have more clear solution.

    Make a recursive function with two arguments: Create(i, count), where i — metal, and count — required mass of the metal.

    If C[i] >= count, let C[i] -= count and return true.

    Elsewhere we will spend all C[i] of metal, and make recursive calls for producing count — C[i] of two metals: Ri1 and Ri2.

    Finally, run a binary search of maximum possible value of count.

    Update: this solution will get TL on special test, see explanation below.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I could come up with binary search and function create but I couldn't avoid going to the same vertex several times. Thx for help.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it

        I have a "used mark" array, like in DFS.

        If there is not enough metal, set used[i] = true before recursive call.

        In the beginning of function check used[i], if used[i] == true, then we have a cycle and function returns false.

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
          ← Rev. 2   Vote: I like it +5 Vote: I do not like it

          Do you set used back to false when returning? If not I don't understand how it implies cycle. If yes, I don't understand why it's fast enough for last test case

          → Reply
          • »
            »
            »
            »
            »
            »
            7 years ago, # ^ |
            ← Rev. 2   Vote: I like it 0 Vote: I do not like it

            Yes, of course.

            It passes all tests :)

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              7 years ago, # ^ |
                Vote: I like it +28 Vote: I do not like it

              Well, I do understand that it passed all tests, but I'd like to know any explanation why it's fast enough if you (or somebody else) have it.

              → Reply
              • »
                »
                »
                »
                »
                »
                »
                »
                7 years ago, # ^ |
                ← Rev. 5   Vote: I like it +15 Vote: I do not like it

                Yes, you are right, my solution will get TL on test like this:

                99
2 3
4 5
4 5
6 7
6 7
8 9
8 9
...
98 99
98 99
1 2
1 2
0 0 0 0 0 .... 0 0 1000000000 1000000000
                → Reply
              • »
                »
                »
                »
                »
                »
                »
                »
                7 years ago, # ^ |
                ← Rev. 2   Vote: I like it -15 Vote: I do not like it

                It is fast because when we are moving to the "child metals" recursively, we are spending all the metals of the current vertex, and "capacity of current metal" becomes zero.

                So at each step, only one of the two events occur: 1)not moving further on recursion tree. 2)setting capacity of current metal to 0 and move recursively.(to the adjacent vertex-metal)

                So, this step2 actually corresponds to marking a vertex as "visited" and recursing on a dfs tree. And whole algorithm corresponds to checking whether or not there is a cycle on this tree.

                → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          But why? Maybe we will need more metal [i] if we ran out of metal [j].

          → Reply
»
7 years ago, # |
← Rev. 3   Vote: I like it +25 Vote: I do not like it

So I tried just implementing all visible sets for 39 points to qualify.

Apparently in B, if you do a binary search, fixing you a set size, and then iterate over all segments of that size, and checking in each one whether there condition holds in O(N) time, that passes the hidden test set. That's like O(N^2 log N). Wat.

UPD: I mean, yes, the final check was more clever than naive O(N) and I was stopping as soon as contradiction was found, but still.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    is there a better complexity for checking a window under O(N)?

    → Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

How comes O(n^2) works for the second problem?

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    Didn't work for me :/

    edit: added another simple break and it passes now

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    lol . Can't believe my O(n^2) solution got accepted .

    → Reply
»
7 years ago, # |
  Vote: I like it +5 Vote: I do not like it

Weak testcases in Task 2?
My O(N^2) solution got accepted (Code: #Y6Epdr)

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +43 Vote: I do not like it

    Google's compilers have optimizations that turn trivial O(N^2)-s to O(N)

    → Reply
»
7 years ago, # |
  Vote: I like it +52 Vote: I do not like it

Surprisingly hard problems for R1. The second problem is almost as hard as GCJ Finals 2013 D.

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it +31 Vote: I do not like it

    I had one hour for the contest and got zero points :/

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 2   Vote: I like it +6 Vote: I do not like it

      Just curious, on which problem were you stuck?

      → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +3 Vote: I do not like it

      Me too (( Maybe a Hookah before the contest would improve our performance :P

      → Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 3   Vote: I like it +16 Vote: I do not like it

    Maybe it's just for me but the second one seems quite easy, just a routine DS.

    Let s[i][0] = Di + Ai, s[i][1] = Di - Bi (why do they give us Di, Ai, Bi instead of direct s[i][0] and s[i][1]?). Just fix a position i from first row and then try to find the longest subarray (l, r) with l ≤ i ≤ r and cardinal of set {s[j][1] | l ≤ j ≤ r, s[j][0] ≠ s[i][0]} must be at most 1. Actually there are at most 2 valid intervals, the one with max prefix (from i) and the one with max suffix (also from i). To not overcount the pairs just store all of them in a set.

    Now just consider a segment-tree with nodes such that for any interval you can find if all the numbers in this interval are equal, the jth number is initially equal to s[j][1]. So basically when you consider all positions i with s[i][0] = t (for fixed t) you delete them and then easily find the intervals in or 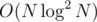by binary search.

    The code gets AC

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +12 Vote: I do not like it

    Standard DP worked in this problem.

    NextM[i]-maximum index, such that all indexes i,i+1,...,NextM[i] have the same M. NextN[i]-maximum index, such that all indexes i,i+1,....,NextN[i] have the same N.

    Let AnsM[i] be the maximum length of the continuous subsequence, starting at i and i'th sign being judged based on "M". AnsN[i] defined similarly.

    Then AnsM[i] is either:

    1)NextM[i]-i+1

    2)NextN[NextM[i]+1]-i+1, if NextM[i] is not last element of array.

    3)AnsN[NextM[i]+1], if M value of i'th index and (NextN[NextM[i]+1]+1)'th index are equal.

    We should traverse from right to left and fill the arrays.

    → Reply
»
7 years ago, # |
  Vote: I like it +14 Vote: I do not like it

how to solve A? I've solved all b and all c and spent most of the time on A with no idea on how to solve it (feeling dumb)

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +9 Vote: I do not like it

    I kept a priority queue of the distances to the point where each number gets rounded up and always incremented the one with the smallest dist.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +6 Vote: I do not like it

      I did the same but got a wrong answer, maybe it's an implementation problem :(

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it

        Yea, I followed that logic too but it did not pass and I could not find my mistake. Yassin can you elaborate your idea ?

        UPD: https://pastebin.com/3zNXhdM8 Here is my source that did not pass.

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it +8 Vote: I do not like it

          Not sure if you handle new elements correctly: you should push (N — sum) zeroes to C to allow for new elements

          → Reply
          • »
            »
            »
            »
            »
            »
            7 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            I push (N — sum) of smallest 'good number'. Why should I push zero ? In priority queue we want to include the 'distance' until we create a number that rounds up, right ?

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              7 years ago, # ^ |
                Vote: I like it +8 Vote: I do not like it

              Yeah, but we can also start a new number (vote for a new programming language) and get that to roundup

              → Reply
              • »
                »
                »
                »
                »
                »
                »
                »
                7 years ago, # ^ |
                  Vote: I like it 0 Vote: I do not like it

                So you say that we can use two steps. 1) Create the language 2) Round it up

                If I understand it correctly, how is that different from round it up immediately to the closest 'good number'

                → Reply
                • »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  7 years ago, # ^ |
                  ← Rev. 2   Vote: I like it +3 Vote: I do not like it

                  Ok, I misunderstood your code.

                  Check this case, I think the first if in your toRound is wrong, remove it.

                  1 8 3 1 1 1

                  → Reply
                • »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  7 years ago, # ^ |
                    Vote: I like it 0 Vote: I do not like it

                  It does not change anything if I remove the 1st if. In your sample my code gives "104" as answer. Is that correct ?

                  → Reply
                • »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  7 years ago, # ^ |
                    Vote: I like it +3 Vote: I do not like it

                  Yes, but with that if it gave 96 on my machine. And if you calculate toRound with N=8 and value=1 it is clearly wrong.

                  → Reply
                • »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  7 years ago, # ^ |
                    Vote: I like it 0 Vote: I do not like it

                  How is it possible to give in your machine different answer ? Are you talking for this "if ((value * 1000) % N == 0)" ? Even if I remove it, it will return the same value in the end and I don't get why you say that it will be wrong.

                  → Reply
                • »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  7 years ago, # ^ |
                    Vote: I like it +6 Vote: I do not like it

                  The version on pastebin returns 12 for value=1, N=8 and it should be 13. That's because the first if is fulfilled, but the second one should be executed, I even checked that by hand.

                  → Reply
                • »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  »
                  7 years ago, # ^ |
                    Vote: I like it 0 Vote: I do not like it

                  Yes, you are right. But still, it gets WA. So probably I miss something else too.

                  → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +31 Vote: I do not like it

      I doubt if greedy with priority_queue is correct. Essentially, you want to compute convolution of polylines, and priority_queue works if those polylines are convex functions, but this is not the case.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        I can't understand, can you give a counter-example?
        Isn't it optimal to increase those with maximal a mod b, if our task is to maximize sum of floor(a / b)?

        → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it +71 Vote: I do not like it

        The official analysis says:

        For each language, we will either be rounding the percentage up or down. We get the maximum answer when as many of these as possible are rounded up.

        But this is not correct. For example, if N = 1000,

        • If the distribution of languages are 8, 8, 8, 8, 968, five are rounded up, and the sum is 101.
        • If the distribution of languages are 5, 5, 5, 985, only four are rounded up, but the sum is 102.

        Alternative proved solution: see the solution for test set 2. It says:

        for a > 1, f(a, b) = max (Ca ≤ i ≤ b) (round(i / N × 100) + f(a — 1, b — i))

        When N ≥ 200, we can prove that we need to consider only two values for i: Ca and Ca + 1.

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Yeah, but I would never increment past roundup. So if the starting value is <= 5, I will stop at 5 and not go to 8.

          → Reply
          • »
            »
            »
            »
            »
            »
            7 years ago, # ^ |
              Vote: I like it +31 Vote: I do not like it

            Yes, I don't know a particular counter-example, it just illustrates that the correctness is non-trivial.

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              7 years ago, # ^ |
              ← Rev. 2   Vote: I like it +31 Vote: I do not like it

              I think they meant above newly getting rounded up numbers.They wanted to maximise it. Also cant we argue the correctness with an exchange argument like something worser got more users then we can say we cant get better off than giving them to this language.

              → Reply
            • »
              »
              »
              »
              »
              »
              »
              7 years ago, # ^ |
                Vote: I like it 0 Vote: I do not like it

              Yes, this also confused me. It is only true when you can add new languages (something I missed when I first read the problem).

              → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        I can't see how it could possibly be better to increment an element that will take longer to reach roundup. I have no clue about your argument though.

        → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it +4 Vote: I do not like it

        Can you elaborate on what do you mean by convolution of polylines?

        → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +10 Vote: I do not like it

    Relative order of c remain the same, so only largest ~200 elements will contribute to the answer.
    Then, do dp[i][p] -- minimal number of votes to get p percents after first i elements.

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    What I did was maintain all distances from the nearest point in sorted order. And also insert new languages with value 0 (since new language no one selected yet) and its distance calculated similarly. Then I just greedily assigned the remaining people

    → Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it +10 Vote: I do not like it

    I think that simply greedy works:

    let qi + ri / n = 100 * ci / n and let q + r / n = 100 / n. Let V = N - c1 - c2 - ..cl.

    It is obvious that the answer is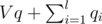 + #{rounds up}.

    Now sort all ri and push infinite stream of zeros at the end. And let process them from biggest to smallest. if ri ≥ n / 2 then ans++, It is better to not vote for this language anymore. if ri < n / 2 give votes (r_i+=r, v--) as long as ri < n / 2.

    In this way we will get the most rounds-up in the formula above.

    → Reply
»
7 years ago, # |
  Vote: I like it +10 Vote: I do not like it

I fixed the first testset, but the rest was skipped anyway, is it ok?

Girl in a jacket

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I'm having the same issue... Hopefully this gets resolved soon.

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    Isn't that simply "Not solved" sign? I think after the end, "WA" and "Skipped testing" have the same icon.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      It was The judgment was skipped. during the contest and now too.

      Actually, I resubmitted my code after seeing this and it was judged correctly.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
        ← Rev. 2   Vote: I like it +46 Vote: I do not like it

        Well, at least it's now easier to compete in Code Jam from Chromebooks...

        On a serious note, make sure to write them an e-mail to notify them of an issue.

        → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

is A a priority queue problem?

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

After reading O(n) solution for B I still dont get it ... (O(nlgn) DnK is understandable though)

Should've wrote a O(n^2) solution in C for B.

Priority queue (map) worked for me in A.

Feels good to get #86 after sucking absolutely **** and getting only #2000 in R1A.

→ Reply
»
7 years ago, # |
  Vote: I like it +26 Vote: I do not like it

I submitted the straightforward LP relaxation for problem C, took the floor of my result, and got AC on small + 1st large case.

Can anyone explain why this is correct / incorrect?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    Your solution idea is correct.

    Proof: Suppose we allow using recipes non-integer amount of times. Consider a solution which

    1. Creates a maximal integer amount of lead.
    2. Minimizes the total number of recipes that are used at least once. (Out of solutions satisfying (1).)
    3. Minimizes the total number of recipes that are used a fractional number of times. (Out of solutions satisfying (1) and (2).)

    Suppose by contradiction that this extremal solution uses a recipe a non-integer number of times.

    Consider the graph G of recipe usage (There is an edge x → y iff x is an ingredient in some used recipe that produces y.). If G contains a cycle, we could reduce the total recipe usage along it until a recipe is no longer used, contradicting the minimality (2). Hence G is acyclic, so we can find a topological ordering of it where all edges of used recipes point to the left.

    Let u be the leftmost node whose creation recipe was used a non-integer amount of times. As all used recipes point to the left and u was leftmost, all recipes it was involved in were used an integer number of times. Thus the fractional part of the recipe of u went to waste. (It wasn't used in any other recipe and if u is lead it wasn't used for the answer as the answer is an integer. Moreover it couldn't sum up with some other fractional part to an integer as there is only a single recipe creating u and the initial supply is an integer.) We could thus reduce the amount we we used the recipe creating u to the next lower integer without creating deficits. This contradicts the minimality (3) of the solution.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +11 Vote: I do not like it

      Thank you. I can finally sleep tonight, knowing that my qualification for round 2 was not completely illegitimate.

      → Reply
»
7 years ago, # |
  Vote: I like it +34 Vote: I do not like it

we would need O(S5) time for this solution, which is not sufficient for Test Set 1

My code:

    for (int i = 0; i < n; ++i)
        for (int j = i; j < n; ++j)
            for (int k = i; k <= j; ++k) pr.pb(a[k].d + a[k].a), pl.pb(a[k].d - a[k].b);
            for (auto& r : pr)
                for (auto& l : pl)
                    for (int k = i; k <= j && found; ++k)
                        found &= a[k].d + a[k].a == r || a[k].d - a[k].b == l;

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I did greedy sort for A and it worked for all the cases.

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it +54 Vote: I do not like it

The official editorial for the problem A says:

We can solve this test set with a greedy strategy. For each language, we will either be rounding the percentage up or down. We get the maximum answer when as many of these as possible are rounded up.

It doesn't look correct to me. If percentages are 19.9, 19.9, 19.9, 19.9, 20.4 then 4 of them are rounded up and the sum of rounded values is 100. But if percentages are 19.1, 19.1, 20.6, 20.6, 20.6 then 3 are rounded up and the sum is 101. So we don't really maximize the number of values that are rounded up. What do I miss here?

EDIT: Nevermind, rng_58 asked the same thing in a post above. So far I understand/guess that the analysis is incorrect but the intended solution works for a different reason.

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 4   Vote: I like it +5 Vote: I do not like it

    The greedy approach works for n ≥ 200 (not sure if it works for n < 200). Here's the idea

    Let pct(i) be the rounded percentage for i / n. And adv(i) be the least number such that pct(adv(i)) = pct(i) + 1, i.e. the least number of men required to increase the rounded percentage by 1 (always exists for n ≥ 200)

    The sum we have before determining the unknown is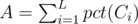 . To increase the answer, let's consider the i-th language. We can add adv(Ci) - Ci to increase percentage by 1, another adv2(Ci) - adv(Ci) to increase by 1 more, another adv3(Ci) - adv2(Ci) for 1 more, and so on...

    The key to the greedy approach is there can be infinitely many new languages, which means we can always add adv(0) to a new language to increase the answer by 1.

    For n ≥ 200, it's easy to prove that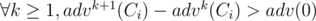 (proof is in comment below). Hence, there's no point to increase a language by two percentages. So the greedy approach works here.

    PS. I actually think this is what the tutorial is trying to say, though they explained it poorly.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 3   Vote: I like it +5 Vote: I do not like it

      Proof:

      adv(0) is the number of men needed to increase percentage from 0% to at least 0.5%. Hence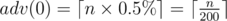

      , the fractional part of advk(p) / n is always between [0.5, 1), let it be B (this is true because for n ≥ 200, each men contributes  ≤ 0.5%. If B is not in this range, you actually need less men, contradiction!)

      Then finally we have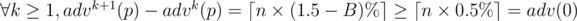

      → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    In both of your cases, you have zero person not-yet-responded. In other words, you can't add anything to any number, since they already add up to 100 (without precision loss). It's basically final state. Generate a test case in terms of the problem input.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I don't claim that was the counter-example to the described solution. I just wanted someone to explain to me that strange lemma.

      → Reply
»
7 years ago, # |
  Vote: I like it +26 Vote: I do not like it

It seems that Google needs to be way more careful with the quality of their tests. A lot of crappy solutions getting accepted is definitely very bad for the competition.

→ Reply
»
7 years ago, # |
← Rev. 6   Vote: I like it +2 Vote: I do not like it

During the contest I wrote the greedy solution for A, but didn't submit it and submitted the DP one because I didn't find a proof for the greedy one. I think it works because:

Let "term" be the fraction part of 100/n (the part after the decimal point). so, whenever you add a user to a language, your net gain (with respect to before adding the user) is either 1-term or -term. so the goal now is to maximize the net gain after all users additions. If term is >= 0.5, adding every user to a new language gives you a 1-term, so it will be the most optimal.

And if term is < 0.5, count the number of users you need for a new language to get the first positive gain (the first roundup), call this count, and add users to already existing languages where you need a number less than count to get the first positive gain (in increasing order of their needed counts). At this point, count will be the least value to get to first positive gain for any language. So, just start iteratively to add a new language and add to it: min(count, left users) until no more users are left.

Example to illustrate what I mean by gain: suppose term is 4/9, if you add a user to a new language, the percentage of this language will be rounded down by 4/9. so your gain here is -4/9 (because before adding user there was no rounding and after adding the user 4/9 was subtracted, so the net is -4/9-0 = -4/9). if a you add another user to the same language, the percentage will be rounded up by 1/9, so your gain here is 5/9 (because before adding user there was down rounding by 4/9 and after adding the user 1/9 was added, so the net is 1/9--4/9 = 5/9)

→ Reply
»
7 years ago, # |
  Vote: I like it +28 Vote: I do not like it

C (Transmutation) can be solved in Θ(M2). We maintain a current recipe for lead and a set of metals that are being replaced due to running out. We alternate the following steps.

  • Create as much lead as possible with the current recipe. (Note that this might be 0.)
  • Take a metal that has insufficient supply. Mark it as replaced and reduce its demand in the recipe to the supply of it by replacing it with some metals that are not marked as replaced.

Step 1 is straight-forward in Θ(M) and step 2 can be implemented in Θ(M) by computing a topological ordering of the metals marked as replaced and then pushing demands down along this ordering. If the topological ordering fails, there is a cycle of forced replacements and we are done. Otherwise this ensures that no new demand will land at a node marked as replaced.

There are at most 2M iterations as every metal will have it's demand reduced at most twice. (First the demand gets reduced to the supply, then the supply drops to 0 when creating lead, so the demand then gets reduced to 0 next.) Hence the runtime is Θ(M2).

→ Reply