alfadel's blog

How to solve SUMPRIM1 — Sum of primes from SPOJ
By alfadel, history, 7 years ago, In English

I'v tried to solve this problem from 4 or 5 days, but the only solution that I'v wrote finish running in 84 seconds using Segmented Sieve.

So is there any hints or resources to start working on the correct solution?

  • Vote: I like it
  • +6
  • Vote: I do not like it

»
7 years ago, # |
  Vote: I like it +1 Vote: I do not like it

You don't actually need to find all primes to cimpute the sum. E.g.here is a description of an approach, that only takes O(n^0.75) time. Link

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    Thank you for the link, but can you explain the method used? because I don't understand it.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 3   Vote: I like it +3 Vote: I do not like it

      What exactly didn't you understand? The only method used here is DP.

      They just define a function that does a bit more than just a summation of the primes. S(v, p) is the sum of all numbers between 2 and v which are still in the sieve if you remove all multiples of all primes  ≤ p. Every non-prime number below n has a factor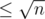 , so the answer to the problem is .

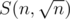      And for this function it is not too hard to come up with a recursive definition. If you don't understand it, just try it with a few numbers. E.g. for S(25, 3), and see what numbers they sum up, and what numbers you sum up with S(25, 3), and which numbers with 3 * S(8, 2) and 3 * S(2, 2).

      Implementation was not described in the link. But I assume that a top-down DP approach is fast enough.

      → Reply