Всем привет!
Университет Иннополис проводит Азиатско-Тихоокеанскую олимпиаду по информатике (Asia-Pacific Informatics Olympiad, APIO) 2018. APIO — это онлайн олимпиада по правилам IOI для школьников из Азиатско-Тихоокеанского региона. Участие в официальном соревновании возможно через представителей олимпиадного комитета страны.
Всех желающих мы приглашаем принять участие в открытом соревновании Open Contest APIO 2018 на том же наборе задач.
Начать контест вы можете в любое удобное время, с 00:00 15 мая 2018 по 00:00 17 мая 2018 (UTC+0). Вам будет предоставлено 3 задачи и 5 часов на их решение. Условия будут доступны на русском и английском языках. Поддерживаемые языки программирования C11, C++14 and Free Pascal. Подробная информация доступна на сайте APIO2018. К сожалению, во время Open Contest не будет возможности задать вопросы по условиям.
Задачи Олимпиады подготовлены niyaznigmatul, qwerty787788, budalnik, izban, PavelKunyavskiy, pashka.
Для участия необходима предварительная регистрация по ссылке. Регистрация закроется 14 мая. После закрытия регистрации вы получите логин и пароль на электронный адрес, который указали при регистрации.
Олимпиада пройдет с использованием проверяющей системы PCMS2.
Ждем вашего участия!
Оргкомитет APIO2018











Will you publish an Editorial after end of the Olympiad?
Organizing Committee won't publish an editorial after the end of the Olympiad. We will publish the tasks, tests and author's solutions on APIO2018 website.
I will give a link for the Olympiad materials here.
Will test data be available after contest? Hopefully this year won't be like the last :P
Everything will be allright:)
We will publish the Olympiad materials until 20 of the May
looked for this types of challenges..thanks :D
Hello, I've already registered 2 days ago. But until now, I didn't get username and password for the contest. Are user and password will be given after registration closed?
Hi, you will get a username and password after the registration closes. I think,we will send all necessary information at 7-8pm(UTC +3).
Can we still register?
Yes, you can.
Sorry for late answer.
Thanks a lot :D
Can those who gave APIO discuss scores if not solutions?
So what about the unofficial results?
Unofficial results?
I'm having a few questions about my solution. Can I post them here now?
wait 2hr
Thanks for reminding, I forgot to convert time of open contest.
So it seems that the online mirror has ended. How to solve 2nd and how to get 1st (I know how to do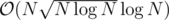 but it won't be fast enough for last subtask).
but it won't be fast enough for last subtask).
Also what's wrong with following solution for 3rd: Compress to bcc. If there is a bridge add esge between the two components. If there is a articular point, split the component such that the AP becomes a new component. Now we have 3 cases — the free vertices are in the same component, 2 vertices are in the same component and all 3 vertices are in different components. This can be done with a couple of DFS-es on the compressed tree. This solution passed for 66 points. Did anyone get AC with a similar idea.
why do you need to split on AP btw? because.. in any case.. after creation of a bridge tree, there will be no case that is not eliminated by the bridge tree but eliminated by the AP-splitting. What i mean is.. if S,F where on different sides of AP then its all good. And even if they are on the same side, We can still go form S, through the AP(which is taken to be C) and then to F, without revisiting. if we were indeed revisiting, then that means there was only one path.. which is again a bridge, and so that case is already eliminated by the bridge tree.
Please correct if wrong.
Test:
6 5
1 2
2 3
3 1
1 4
4 5
5 1
If we don't split, we might count tuples like (1, 4, 2).
Thanks. got it.
Sorry for my poor English
2nd problem can be solved in the following way: First, consider how to solve subtask 4(all circles have the same radius R): We can divide the Cartesian plane by square with R*R. Then, for each circle i that has not been removed yet, let's denote the circle i in block x_i, y_i. Other circles which might be removed by circle i must be in block ( x_i ± 2 , y_i ± 2 ).
Now, let’s try to solve the whole task. Let’s denote one operation as: one circle i remove other circles in blocks ( x_i ± 2 , y_i ± 2 ). First, let’s sort the circles by the radius. Let’s divide the Cartesian plane with R = r_max. Then do the operation. If the operation had be done more than 1024 times and now the current r * 100 <= r_max. Then we set r_max = r and divide the Cartesian plane with new radius r_max again. The source of parameter 1024 and 100 is found during the contest. (If the parameter 1024 is changed to 3000 or more, it will TLE on test 88).
I got AC on 2nd problem by the above method.
Electrical God<(_ _)>
Instead of dividing into R*R blocks, we can divide blocks using logs.
Assume that at first, we have one big block, with coordinate [0,0] to [2^32, 2^32]
At each query, we can just divide each block into 2*2 smaller block until the side of each block is as small as possible but still bigger than current R. The rest of the solution is same as yp155136's one.
Please note that the division step can be done quickly using bitwise operator, combined with the idea of radix sort (base 2)
By using this method, we do not need to find the "magic" value for each division.
For Prob C, I got AC with an idea similar to radoslav11, however, I connect every nodes in one BCC to a virtual nodes so that I need to do DFS just one time.
As I said above, I have a few questions about my solution for the 1st problem.
During the contest, I came up with a O(N * log * log) solution with a segment tree where each of its node is a set. And I known that my solution was much slower than the author's one but 5 seconds for time limit made me believe that it would pass.
But not as I expected, my solution was only able to pass N < 60000 subtasks and got TLE with others. So I accepted that my solution was too slow and tried to solve the two first N < 300000 ones in O(Nlog).
And again, I got TLE. But what make me confused is I passed only one of them.
So I want to ask if the test cases for the first N < 300000 was weak and why a simple O(Nlog) solution with segment tree can not pass the problem in 5 seconds time limit. Thanks for reading.
What was your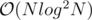 approach?
approach?
First of all, sorry for my poor English.
I sorted both the stores and queries in increasing order of the year.
In a simple approach, for each of K types of stores, we'll maintain a set of the stores and we only need to binarysearch for its closest store in the set for each query.
Let's call the set K closest stores of K different type to the position x is s(x). Now we'll have to maintain a segment tree which can maintain min(s(x)) and max(s(x)).
If K = 1, it would be easy to insert and delete stores from by just implementing a lazy propagation segment tree.
If we only delete stores, we can use a max-min segment tree.
But for the last subtask, since we only need to know the min(s(x)) and max(s(x)), for each node p on segment tree which covers the range [L, R], we'll maintain a set of stores T(p) such that if a store r is in T(p) then r is also in s(i) with every L <= i <= R. We can easily see that we don't need to perform lazy updates on this segment tree. For each inserting and deleting update on range [X, Y], we should stop going deeper inside subtree p if X <= L <= R <= Y and perform the update on T(p). Then for each asking query of postion x, we can calculate the answer with every node p such that L <= x <= R.
You can actually remove the set, using 2 priority queues and 2 vectors to keep the things you should erase. This way it should be much faster. Thanks btw.
Actually, I thought about that during contest, using priority queue for pair < position, the index of the store >. But since I was not able to pass the O(Nlog) one, I gave up the contest.
When'll the organizing committee publish the dataset ?
Hi!
We will publish the Olympiad materials until 20 of the May
thanks
It's 20 of the May today, Where's the link
found it on the official website
Shouldn't a N*root(N) solution pass for 30 points in problem 2? I tried it but somehow got TLE.
Code: https://pastebin.com/kC1u1tEv
Just imagine when vec.size()>=blocksize happens all the time. This is pure n^2.
As usual, all the tasks are ready for judging: https://oj.uz/problems/source/326
Thanks for authors providing a Polygon package, it was really helpful! We hope we could also able to upload APIO 2017 too.
UPD: We mistakenly uploaded tests wrongly (slightly wrong), and we rejudged every solution. Maybe your score has been changed. Sorry for the inconvenience caused.