Codeforces Round #486 (Div. 3) Editorial

#	User	Rating
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

#	User	Contrib.
1	cry	167
2	Um_nik	163
3	maomao90	162
4	atcoder_official	161
5	adamant	159
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
9	Dominater069	153
9	nor	153

Tutorial

Solution (Vovuh)

#include <bits/stdc++.h>

using namespace std;

int main() {
#ifdef _DEBUG
	freopen("input.txt", "r", stdin);
//	freopen("output.txt", "w", stdout);
#endif
	
	int n, k;
	cin >> n >> k;
	set<int> el;
	vector<int> ans;
	for (int i = 0; i < n; ++i) {
		int x;
		cin >> x;
		if (!el.count(x)) {
			ans.push_back(i);
			el.insert(x);
		}
	}
	
	if (int(ans.size()) < k) {
		cout << "NO\n";
	} else {
		cout << "YES\n";
		for (int i = 0; i < k; ++i)
			cout << ans[i] + 1 << " ";
		cout << endl;
	}
	
	return 0;
}

988B - Substrings Sort

Tutorial

Solution (Vovuh)

#include <bits/stdc++.h>

using namespace std;

int main() {
#ifdef _DEBUG
	freopen("input.txt", "r", stdin);
//	freopen("output.txt", "w", stdout);
#endif
	
	int n;
	cin >> n;
	vector<string> s(n);
	for (int i = 0; i < n; ++i)
		cin >> s[i];
		
	sort(s.begin(), s.end(), [&] (const string &s, const string &t) {
		return s.size() < t.size();
	});
	
	for (int i = 0; i < n - 1; ++i) {
		if (s[i + 1].find(s[i]) == string::npos) {
			cout << "NO\n";
			return 0;
		}
	}
	
	cout << "YES\n";
	for (auto it : s)
		cout << it << endl;
	
	return 0;
}

988C - Equal Sums

Tutorial

Solution (Vovuh)

#include <bits/stdc++.h>

using namespace std;

int main() {
#ifdef _DEBUG
	freopen("input.txt", "r", stdin);
//	freopen("output.txt", "w", stdout);
#endif
	
	int k;
	cin >> k;
	vector<pair<int, pair<int, int>>> a;
	for (int i = 0; i < k; ++i) {
		int n;
		cin >> n;
		vector<int> x(n);
		for (int j = 0; j < n; ++j)
			cin >> x[j];
		int sum = accumulate(x.begin(), x.end(), 0);
		for (int j = 0; j < n; ++j)
			a.push_back(make_pair(sum - x[j], make_pair(i, j)));
	}
	
	stable_sort(a.begin(), a.end());
	for (int i = 0; i < int(a.size()) - 1; ++i) {
		if (a[i].first == a[i + 1].first && (a[i].second.first != a[i + 1].second.first)) {
			cout << "YES" << endl;
			cout << a[i + 1].second.first + 1 << " " << a[i + 1].second.second + 1 << endl;
			cout << a[i].second.first + 1 << " " << a[i].second.second + 1 << endl;
			return 0;
		}
	}
	
	cout << "NO\n";
	
	return 0;
}

988D - Points and Powers of Two

Tutorial

Solution (Vovuh)

#include <bits/stdc++.h>

using namespace std;

int main() {
#ifdef _DEBUG
	freopen("input.txt", "r", stdin);
//	freopen("output.txt", "w", stdout);
#endif
	
	int n;
	cin >> n;
	vector<int> x(n);
	for (int i = 0; i < n; ++i) {
		cin >> x[i];
	}
	
	sort(x.begin(), x.end());
	vector<int> res = { x[0] };
	
	for (int i = 0; i < n; ++i) {
		for (int j = 0; j < 31; ++j) {
			int lx = x[i] - (1 << j);
			int rx = x[i] + (1 << j);
			bool isl = binary_search(x.begin(), x.end(), lx);
			bool isr = binary_search(x.begin(), x.end(), rx);
			if (isl && isr && int(res.size()) < 3) {
				res = { lx, x[i], rx };
			}
			if (isl && int(res.size()) < 2) {
				res = { lx, x[i] };
			}
			if (isr && int(res.size()) < 2) {
				res = { x[i], rx };
			}
		}
	}
	
	cout << int(res.size()) << endl;
	for (auto it : res)
		cout << it << " ";
	cout << endl;
	
	return 0;
}

988E - Divisibility by 25

Tutorial

Solution (Vovuh)

#include <bits/stdc++.h>

using namespace std;

const int INF = 1000 * 1000 * 1000;

int main() {
#ifdef _DEBUG
	freopen("input.txt", "r", stdin);
//	freopen("output.txt", "w", stdout);
#endif
	
	long long n;
	cin >> n;
	
	string s = to_string(n);
	
	int ans = INF;
	
	int len = s.size();
	for (int i = 0; i < len; ++i) {
		for (int j = 0; j < len; ++j) {
			if (i == j) continue;
			string t = s;
			int cur = 0;
			for (int k = i; k < len - 1; ++k) {
				swap(t[k], t[k + 1]);
				++cur;
			}
			
			for (int k = j - (j > i); k < len - 2; ++k) {
				swap(t[k], t[k + 1]);
				++cur;
			}
			
			int pos = -1;
			for (int k = 0; k < len; ++k) {
				if (t[k] != '0') {
					pos = k;
					break;
				}
			}
			
			for (int k = pos; k > 0; --k) {
				swap(t[k], t[k - 1]);
				++cur;
			}
			
			long long nn = atoll(t.c_str());
			if (nn % 25 == 0)
				ans = min(ans, cur);
		}
	}
	
	if (ans == INF)
		ans = -1;
		
	cout << ans << endl;
	
	return 0;
}

988F - Rain and Umbrellas

Tutorial

Solution (Vovuh)

#include <bits/stdc++.h>

using namespace std;

const int INF = 1000 * 1000 * 1000;

int main() {
#ifdef _DEBUG
	freopen("input.txt", "r", stdin);
//	freopen("output.txt", "w", stdout);
#endif
	
	int a, n, m;
	cin >> a >> n >> m;
	vector<int> rain(a + 1);
	vector<pair<int, int>> umb(a + 1, make_pair(INF, -1));
	vector<int> costs(m);
	
	for (int i = 0; i < n; ++i) {
		int l, r;
		cin >> l >> r;
		for (int j = l; j < r; ++j)
			rain[j] = 1;
	}
	
	for (int i = 0; i < m; ++i) {
		int x, p;
		cin >> x >> p;
		costs[i] = p;
		umb[x] = min(umb[x], make_pair(p, i));
	}
	
	vector<vector<int>> dp(a + 1, vector<int>(m + 1, INF));
	dp[0][m] = 0;
	for (int i = 0; i < a; ++i) {
		for (int j = 0; j <= m; ++j) {
			if (dp[i][j] == INF)
				continue;
			if (rain[i] == 0)
				dp[i + 1][m] = min(dp[i + 1][m], dp[i][j]);
			if (j < m)
				dp[i + 1][j] = min(dp[i + 1][j], dp[i][j] + costs[j]);
			if (umb[i].first != INF)
				dp[i + 1][umb[i].second] = min(dp[i + 1][umb[i].second], dp[i][j] + umb[i].first);
		}
	}
	
	int ans = INF;
	for (int i = 0; i <= m; ++i)
		ans = min(ans, dp[a][i]);
	if (ans == INF)
		ans = -1;
	cout << ans << endl;
	
	return 0;
}

Solution (step_by_step)

//#pragma comment(linker, "/stack:200000000")
//#pragma GCC optimize("Ofast")
//#pragma GCC target("sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx,avx,tune=native")
//#pragma GCC optimize("unroll-loops")
 
#include <stdio.h>
#include <bits/stdc++.h>
 
#define uint unsigned int
#define ll long long
#define ull unsigned long long
#define ld long double
#define rep(i, l, r) for (int i = l; i < r; i++)
#define repb(i, r, l) for (int i = r; i > l; i--)
#define sz(a) (int)a.size()
#define fi first
#define se second
#define mp(a, b) make_pair(a, b)
 
using namespace std;
 
inline void setmin(int &x, int y) { if (y < x) x = y; }
inline void setmax(int &x, int y) { if (y > x) x = y; }
inline void setmin(ll &x, ll y) { if (y < x) x = y; }
inline void setmax(ll &x, ll y) { if (y > x) x = y; }
 
const int N = 2001;
const int inf = (int)1e9 + 1;
const ll big = (ll)1e18 + 1;
const int P = 239;
const int MOD = (int)1e9 + 7;
const int MOD1 = (int)1e9 + 9;
const double eps = 1e-9;
const double pi = atan2(0, -1);
const int ABC = 26;

struct Line
{
    ll k, b;
    Line() {}
    Line(ll k, ll b) : k(k), b(b) {}
    ll val(ll x) { return k * x + b; }
};

int cnt_v;
Line tree[N * 4];

void build(int n)
{
    cnt_v = 1;
    while (cnt_v < n)
        cnt_v <<= 1;
    rep(i, 0, cnt_v * 2 - 1)
        tree[i] = Line(0, inf);
}

void upd(int x, int lx, int rx, int l, int r, Line line)
{
    if (lx >= r || l >= rx)
        return;
    else if (lx >= l && rx <= r)
    {
        int m = (lx + rx) / 2;
        if (line.val(m) < tree[x].val(m))
            swap(tree[x], line);
        if (rx - lx == 1)
            return;
        if (line.val(lx) < tree[x].val(lx))
            upd(x * 2 + 1, lx, (lx + rx) / 2, l, r, line);
        else
            upd(x * 2 + 2, (lx + rx) / 2, rx, l, r, line);
    }
    else
    {
        upd(x * 2 + 1, lx, (lx + rx) / 2, l, r, line);
        upd(x * 2 + 2, (lx + rx) / 2, rx, l, r, line);
    }
}

ll get(ll p)
{
    int x = p + cnt_v - 1;
    ll res = tree[x].val(p);
    while (x > 0)
    {
        x = (x - 1) / 2;
        setmin(res, tree[x].val(p));
    }
    return res;
}

int add[N];
int best[N];

ll dp[N];

int main()
{
    //freopen("a.in", "r", stdin);
    //freopen("a.out", "w", stdout);
    ios_base::sync_with_stdio(0);
    cin.tie(0);
    cout.precision(20);
    cout << fixed;
    //ll TL = 0.95 * CLOCKS_PER_SEC;
    //clock_t time = clock();
    int L, n, m;
    cin >> L >> n >> m;

    rep(i, 0, n)
    {
        int l, r;
        cin >> l >> r;
        add[l]++;
        add[r]--;
    }
    rep(i, 1, L + 1)
        add[i] += add[i - 1];

    fill(best, best + L + 1, inf);
    rep(i, 0, m)
    {
        int x, p;
        cin >> x >> p;
        setmin(best[x], p);
    }

    // dp[i] + best[i] * (j - i) = best[i] * j + (dp[i] - best[i] * i)
    build(L + 1);
    fill(dp, dp + L + 1, inf);
    dp[0] = 0;
    upd(0, 0, cnt_v, 0 + 1, cnt_v, Line(best[0], dp[0] - best[0] * 0));
    rep(i, 1, L + 1)
    {
        dp[i] = get(i);
        if (add[i - 1] == 0)
            setmin(dp[i], dp[i - 1]);
        upd(0, 0, cnt_v, i + 1, cnt_v, Line(best[i], dp[i] - best[i] * i));
    }
    cout << (dp[L] != inf ? dp[L] : -1) << "\n";
    return 0;
}

| #486 (Div. 3) | #485 (Div. 2) | #484 (Div. 2) | #483 (Div. 2) | #482 (Div. 2) | #481 (Div. 3) ------------------------------------------------------------------------------------------------- A | 3308 | 4140 | 2291 | 3879 | 3503| 2493 B | 2460 | 2763 | 2175 | 2952 | 636| 2508 C | 1313 | 1963 | 1416 | 743 | 1362| 2139 D | 292 | 600 | 370 | 392 | 130| 777 E | 64 | 501 | 14 | 9 | 7| 1066 F | 18 | 8 | 3 | - | -| 824 G | - | - | - | - | -| 261

Comments (75)

Show archived | Write comment?

ghoshsai5000

6 years ago, # |

Can you explain a bit about what the Convex Hull Trick and Li Chao tree are ? Most Div 3 contestants like myself have little-to-no idea about what they are :)

→ Reply

awoo

6 years ago, # ^ |

Check this article

vovuh

Also check the solution by step_by_step which uses Convex Hull Trick and Li Chao tree (I added it to the tutorial)

Kaszper

← Rev. 3 →

Are you sure that it works in n*log^2(n)? In my opinion it's n*log(n). Why is it log^2?

Does it also use Convex Hull in some way?

In my opinion the tree can: 1. Given a and b, insert a new linear function. 2. Given x0, print the maximum value f(x0).

and it is done in a*log(a)

It depends on solution. Solution by step_by_step works in O(n*log^2(n)), but there are another one solution that works in O(n*log(n)) (of course there are many solutions which works in O(n*log^2(n)), O(n*log(n)) and with many other complexities). I was describe one of them and i do not deny that in this problem exists solution in O(n*log(n)).

Thanks for reply. Could you tell me why it’s log(n)^2? Does update on the tree take log^2? I can’t see why.

step_by_step

This segment tree does the following:
1) splits the query segment into log(n) segments (like all segment trees do)
2) From each of these log(n) segments it goes down until it reaches the leaf, so for each segment it spends log(n) operations (the height of tree)

If n = 2^k and the query segment is [0, 2^k — 2] then the number of operations will be (log(n) — 1) + (log(n) — 2) + (log(n) — 3) + ... = O(log(n)^2)

Thanks, I understand now. So all Li Chao trees work in log(n)^2?

← Rev. 2 →

No, if the size of segment tree is power of two and you update all elements then it works in O(log(n))

So you can use it when you need Convex Hull Trick and the query coordinates are not big. Time complexity will be log(a) per update/query, where a is the minimal power of two greater than maximal coordinate.

So if I make updates on whole tree, then updating works in log(n), because I divide it into one segment and it goes down one way to leaf. So log(n). And query costs log(n) (from root to leaf).

If I change updating to whole tree, then it will work in a*log(a).

Yes, it will be O(a*log(a))
While writing my solution I didn't notice it)

hackerwizard

Can we use this when the query coordinates are negative but their absolute value<=10^5?

Yes, you can add 10^5 to all your coordinates and change linear functions:
k*x+b -> k*(x+10^5)+b-k*10^5

Thank you,just one more question suppose there are n linear functions and for a given query we consider only functions from l to r. So can we use lichao tree in this problem?

dmkz

← Rev. 4 →

Hard contest for Div3, I think that it is Div2. Statistics of successful solutions in comparison with previous Div3 and Div2 confirms this

Can you share the statistics ?

Updated

+25

Maybe it's not that this round was too hard but the previous ones were too easy?

pantw

Almost all my school mates are complaining about the round.

I think maybe it's a bit too hard for division 3?

Easier than div.2 rounds, but definitely harder than what I thought div.3 round should be.

+18

There are no really hard problems, even the problems E and F are close to typical Div2C problems, but not harder than Div2C. If i will make Div3 rounds much easier, it will lead to easy way to get 1600+ by participating in Div3 rounds.

alwerty

All problems were doable and I liked them, but I think there is too little difference in difficulty form C to F

I would agree with you that the difficulty of E and F were quite normal.

However C and D might be of inappropriate difficulty.

What's more, STLs like map, vector or set shouldn't appear so frequently since the beginners may not make their way to STL so fast.

My solutions for C and D are almost don't use STL expect sort and standard binary search method. This is not too hard to implement your own sort or your own binary search to find the element in O(log n) instead of O(n).

But I agree with you that C and D should be much easier that they were in this round. And in these problems must not be too difficult ideas or algorithms as fast sorting or binary search.

Player.01

-22

Reading your comment vovuh : I wonder , why Div-3 was even created!

+42

Reading your comments Player.01: I wonder that you first ask to make the problems harder, and when I did it, you wonder that they are too hard.

-12

My intention was to remind the setters that the logic behind creating Div-3 , which is not surely pulling them to Div-2 comfortably , but to set problems that would help them to train logically & rigorously. I mean , it should work as a guideline , don't you think? I believe , setters must be flexible to any feedback & take only the logical ones into considerations rather blindly defending his rounds. Thnx for reading my comments. Have a nice day!

+10

Please don't think that I'm blindly defend my rounds. I'm accept some good ideas from comments and draw my conclusions to do the rounds better than they are now. Have a nice day and sorry if I'm offended you.

You also doesn't notice that there are different parts of community participate in div2 and in div3.

From your post : " Probably, participants from the first division will not be at all interested by this problems. And for 1600-1899 the problems will be too easy."

I am pretty sure Not all Div-2 participants solved All the "too esay" problems , even some Div-1 participants struggled with E & F .

ShafinKhadem

Maybe some div-1 participants didn't solve E & F. But that doesn't prove that they struggled with E & F. It may also happen that they found E & F too easy to try. I personally found D to be tougher than E & F. F was very basic DP problem. E was also simple, just handling corner cases were difficult. I haven't learnt anything by solving E & F. But I have learnt from D.

hyena

Can anyone please explain the use of npos in solution B — "if (s[i + 1].find(s[i]) == string::npos) " ?

Cplusplus.com says that it is the greatest possible value for an element of size_t , What does it means ?

It is almost the same as -1 (means "not found" or some similar). I use it just because of my habit. You can replace it with -1 and nothing will change.

I can be wrong and maybe someone else will explain it better than me.

Em00n

Just complementing Vovuh's answer: since npos is unsigned, -1 actually corresponds to the largest possible integer value. Since it's greater than the size of any string, it never equals a valid position, and is thus returned to indicate a failed search.

Citizen404

In solve 988D:

			if (isl && int(res.size()) < 2) {
				res = { lx, x[i] };
			}
			if (isl && int(res.size()) < 2) {
				res = { x[i], rx };
			}

Maybe it would be more correct?:

                        if (isl && int(res.size()) < 2) {
				res = { lx, x[i] };
			}
			if (**isr** && int(res.size()) < 2) {
				res = { x[i], rx };
			}

Woooops, yes, you are right! But surely this solution is also correct and the second if statement is useless :D It is because of you will check this pair of points when x[i] will be the right point and lx will be the left point.

I will fix it anyway, thank you :)

Nothing, but you again made mistake....:

                        if (isr && int(res.size()) < 2) {
				res = { lx, x[i] };
			}
			if (isl && int(res.size()) < 2) {
				res = { x[i], rx };
			}

You need to swap first line and 4th....

Oh, I made the second mistake only in the Russian version of editorial, in English version all is fine :D Thank you, fixed again (I hope :D)

Colossus20

There is any other way to think/solve D?

AkA

vovuh,In problem C why did you use stable_sort? Normal sort also passed. What is the difference? In the future at what kind of situations should we use stable sort?

AishwaryaR

4 years ago, # ^ |

Hi, I've the same doubt, were you able to find an answer?

Nope

Aeon

+21

vovuh in F we can use another dp with O(a) memory and O(a²) time:

in case we have umbrella in i-th position: dp[i] = min i <= j (dp[j] + (j - i) * w[i])
if we don't: dp[i] = min(dp[i + 1], dp[i])

and when doing convex hull trick on this dp, we can see that slopes are decreasing, so we don't need additional structures to maintain convex hull. so this can be solved in O(a * log(a)) time

link: 38904415

JoseSoto

Problem F — Someone can help me?, i can't find mi error :(.

My code

Thanks in advance c:

Emiso

If you have more than one umbrella at the same place, you should get the one with minimum weight

You're right. Oh my god, i can't believe that i didn't consider it. Thank you. :D

kingosak

@Emiso i was having the same mistake. thanks a lot

Informer

In problem D tutorial, how is k equal to L ?

aboAdnan

If we transform to the binary representation, any power of two is represented by 1 and number of 0's (may be zero) to the right of that 1, for example: 1 and 1000, which are equal in decimal to: 1 and 8, respectively.

So, when you sum two different powers of two together, you will get a number which is represented in binary as two 1's and number of 0's (may be zero), for example:

10000

00100

=====

10100

So, the result is not a power of two.

But there is one case that will give us a power of two from summing two powers of two, and it is summing a power of two to itself, like:

01000

Hope it answered.

I_love_to_eat

Thanks for the answer, it cleared a lot. But why does the answer not exceed 3? it could have been dist(a, d) * 4 instead of 3.

upd: ok, I got it, in case of abcde there's still a abcd triplet in there, so the distance between a and c will still be 3*2^k, and it will be still invalid.

Welcome :).

The equation dist(a, d) = dist(a, b) * 3 came from the proofs before it.

In the same way in which the tutorial proved that dist(a, b) = dist(b, c), we can prove that dist(b, c) = dist(c, d). So, the following equation is hold:

dist(a, b) = dist(b, c) = dist(c, d) ( = x, for example).

And we know that: dist(a, d) = dist(a, b) + dist(b, c) + dist(c, d) = x + x + x = 3 * x. And from here, 3 came.

And any changing in this 3 means that some changes in the previous parts of the proof were happened, for example:

dist(a, d) = 4 * x can come from: dist(c, d) = 2 * x, which means that: dist(b, d) = dist(b, c) + dist(c, d) = x + 2 * x = 3 * x, which isn't a power of two, but in the problem, we need dist(b, d) to be equal to a power of two.

ron2794

Can you maybe also answer how the term of 10^9 came in the equation when calculating the complexity?

Sorry, I cannot reply now. I'll try later (may be toworrow).

Jakube

You iterate over all powers of 2, from 2⁰ until 2^x with 2^x ≤ 2 * 10⁹.

There are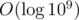 $\text{[math]}$ many of these powers.

Thank you, it would have taken with me much more words to answer it :)

haitun

Will the vector in problem C's solution too large? Cuz it maybe 2 * 1e5 * 2 * 1e5 elements...?

UltimateChoker

Why am i getting TLE on div 3 D when using map, and AC when using original binary search ?

Using binary search: https://codeforces.net/contest/988/submission/38916484

Using STL Map : https://codeforces.net/contest/988/submission/38916424

I have made the same mistake. See this comment please.

Oh thanks alot bro

Single_Ready_To_Mingle

" You can also notice that the order of swaps doesn't matter and you can rearrange them in such a way that no leading zero appears on any step. " How to prove this or any kind of intuition behind this ?

You can rearrange the operations in such a way that first of all you move the leftmost non-zero digit in the number to the left in order to keep the number correct after each of the next operation.

But in general case you don't know which digit will be leftmost non-zero (there are too many cases that are depend on the digits you choose), so to make this problem much simpler you firstly move digits you choose to the right and then find the leftmost non-zero digit and move it to the left.

Yeah Cool, Thanks a lot :)

Yash_Jain

can anyone explain the 3rd case of 988F .

Devil

Test Case:

10 1 1
0 9
1 5

the segment 0-9 is under rain and only haft an umbrella on the position 1 so you never can pass the position 0 without getting wet, so the output is -1

dbhrockzz

Can anyone tell, why http://codeforces.net/contest/988/submission/38851322 this solution didn't work for Problem C?

The approach given in the Editorial also fails in Python.

bukunu

Why does the memory blow up on 7th test case? 38888128 (Problem B)

I know the complexity is O(n2)...but why does memory blow up?

Is it something to do with sorting string array?

orange4glace

https://codeforces.net/blog/entry/59770?#comment-434977

genius_noob

Probably a simple solution to E : http://codeforces.net/contest/988/submission/38965567 As we have only 4 options 00, 25, 50, 75 at the end Just count the place by which these digit is to be moved obviously taking care of leading zeroes at the beginning in case the swap is made.

gokhalesushant65

Can someone explain the problem with this approach for "Rain and umbrellas"?

let - dp[x][0] --> indicates that umbrella was not used for segment (x-1) to (x)

dp[x][1] --> indicates that umbrella was used for segment (x-1) to (x)

Now, dp[x][0]
= infinity (or invalid) --> segment (x-1) to x is under rain

= min( dp[x-1][0], dp[x-1][1] ) --> segment (x-1) to x not under rain

dp[x][1]
= (best wt umbrella uptil now) + dp[x-1][1] --> I continue carrying same umbrella

= (best wt umbrella uptil now) + min( dp[x-1][0], dp[x-1][1] )
--> I drop heavy wt umbrella and pick more lighter umbrella

Getting wrong answer. Not able to find whats wrong with the approach.

rahul_iit

The problem in your approach is best umbrella to be carried till position i may not be necessarily the best one for i+1 but other umbrella might help. For computing the optimal solution, you MUST consider all previous choices of umbrellas. This is the dynamic programming approach, what you BEST is actually greedy. Hope it helps.

luismo

Can anybody help me with this: http://codeforces.net/contest/988/submission/38960067 I can't find my mistake. Is stuck in testcase 5.

In problem F I use:

int dp[i] — the minimmum fatigue to get to position i,

bool rain[i] — true if position i is into a raining interval,

umbrellas[i] — the minimmum weight of an umbrella at position i, if there is no umbrella, umbrellas[i] = 0;

In my approach I calculate for each position i, what's the minimmum fatigue of getting there using the umbrella at position j (j <= i):

dp[i] = min( umbrellas[j] * (i — j) + dp[j — 1]) for each j from i to 0;

I can't see where my idea fails, still stuck in testcase 5.

Not reading carefully the problem caused me multiple WA5, specifically this lines:

he must carry at least one umbrella while he moves from x to x+1 if a segment [x,x+1] is in the rain (i.e. if there exists some i such that li≤x and x+1≤ri).

Hope you don't come across the same mistake

gsparken

about Problem D: why the size of the answer set can be 1?

Complexity_Cutter

5 years ago, # |

Can anyone please tell me how standard compare function works or refer me any article about it?

harsh_it2003

2 years ago, # |

I'm tryna do F using the following approach but I'm getting WA on test 19 :

let the states of dp be the umbrellas. Now dp[i] keeps the minimal fatigue to reach the umbrella i. Now for all umbrellas I've kept the minimal fatigue to reach it. So now say the best or minimal fatigue to reach the destination, when the last umbrella that is used it say k, is dp[k]+(des-k)*weight[k]. Note that the destination is the last rainy segment's end point.

So I'll take the minimum out of all (reaching the destination with K as the last umbrella.)

This looks quite right intuitively but I'm getting WA on test 19. I've been tryna figure it out but couldn't.

Please help.

submission:
https://codeforces.net/contest/988/submission/161450389

vovuh's blog