Разбор Codeforces Round #490 (Div. 3)

№	Пользователь	Рейтинг
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

№	Пользователь	Вклад
1	cry	167
2	Um_nik	163
3	maomao90	162
3	atcoder_official	162
5	adamant	159
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
9	Dominater069	153
9	nor	153

Я сильно сожалею, что задача D оказалась намного сложнее, чем я ожидал, и образовалась пропасть в сложности между задачами C и D. Надеюсь, в следующих раундах такого не повторится.

UPD: Хочу сказать отдельное спасибо kevinsogo за огромную помощь с разборами и с подготовкой раунда в целом.

999A - Mishka and Contest

Разбор

Решение (Vovuh)

#include <bits/stdc++.h>

using namespace std;

int main() {
#ifdef _DEBUG
	freopen("input.txt", "r", stdin);
//	freopen("output.txt", "w", stdout);
#endif
	
	int n, k;
	cin >> n >> k;
	vector<int> a(n);
	for (int i = 0; i < n; ++i)
		cin >> a[i];
	
	int ans = 0;
	while (!a.empty() && a.back() <= k) {
		++ans;
		a.pop_back();
	}
	reverse(a.begin(), a.end());
	while (!a.empty() && a.back() <= k) {
		++ans;
		a.pop_back();
	}
	
	cout << ans << endl;
	
	return 0;
}

999B - Reversing Encryption

Разбор

Решение (Vovuh)

#include <bits/stdc++.h>

using namespace std;

int main() {
#ifdef _DEBUG
	freopen("input.txt", "r", stdin);
//	freopen("output.txt", "w", stdout);
#endif
	
	int n;
	string s;
	cin >> n >> s;
	for (int i = 1; i <= n; ++i) {
		if (n % i == 0) {
			reverse(s.begin(), s.begin() + i);
		}
	}
	cout << s << endl;
	
	return 0;
}

999C - Alphabetic Removals

Разбор

Решение 1 (Vovuh)

#include <bits/stdc++.h>

using namespace std;

int main() {
#ifdef _DEBUG
	freopen("input.txt", "r", stdin);
//	freopen("output.txt", "w", stdout);
#endif
	
	int n, k;
	cin >> n >> k;
	string s;
	cin >> s;
	
	vector<int> cnt(26);
	for (auto c : s) ++cnt[c - 'a'];

	int pos = 26;
	for (int i = 0; i < 26; ++i) {
		if (k >= cnt[i]) {
			k -= cnt[i];
		} else {
			pos = i;
			break;
		}
	}
	
	string ans;
	int rem = k;
	for (auto c : s) {
		int cur = c - 'a';
		if (cur > pos || (cur == pos && rem == 0)) {
			ans += c;
		} else if (cur == pos) {
			--rem;
		}
	}
	
	cout << ans << endl;
	
	return 0;
}

Решение 2 (Vovuh)

#include <bits/stdc++.h>

using namespace std;

int main() {
#ifdef _DEBUG
	freopen("input.txt", "r", stdin);
//	freopen("output.txt", "w", stdout);
#endif
	
	int n, k;
	cin >> n >> k;
	string s;
	cin >> s;

	vector<pair<char, int>> c(n);
	for (int i = 0; i < n; ++i)
		c[i] = make_pair(s[i], i);
	sort(c.begin(), c.end());
	sort(c.begin() + k, c.end(), [&] (const pair<char, int> &a, const pair<char, int> &b) {
		return a.second < b.second;
	});
	
	for (int i = k; i < n; ++i)
		cout << c[i].first;
	cout << endl;
	
	return 0;
}

999D - Equalize the Remainders

Разбор

Решение (Vovuh)

#include <bits/stdc++.h>

using namespace std;

int main() {
#ifdef _DEBUG
	freopen("input.txt", "r", stdin);
//	freopen("output.txt", "w", stdout);
#endif
	
	int n, m;
	cin >> n >> m;
	int k = n / m;
	vector<int> a(n);
	vector<vector<int>> val(m);
	for (int i = 0; i < n; ++i) {
		cin >> a[i];
		val[a[i] % m].push_back(i);
	}
	
	long long ans = 0;
	vector<pair<int, int>> fre;
	for (int i = 0; i < 2 * m; ++i) {
		int cur = i % m;
		while (int(val[cur].size()) > k) {
			int elem = val[cur].back();
			val[cur].pop_back();
			fre.push_back(make_pair(elem, i));
		}
		while (int(val[cur].size()) < k && !fre.empty()) {
			int elem = fre.back().first;
			int mmod = fre.back().second;
			fre.pop_back();
			val[cur].push_back(elem);
			a[elem] += i - mmod;
			ans += i - mmod;
		}
	}
	
	cout << ans << endl;
	for (int i = 0; i < n; ++i)
		cout << a[i] << " ";
	cout << endl;
	
	return 0;
}

999E - Reachability from the Capital

Разбор

Решение (Vovuh)

#include <bits/stdc++.h>

using namespace std;

const int N = 5010;

int n, m, s;
vector<int> g[N];
bool used[N];
bool ok[N];

int cnt;

void dfs1(int v) {
	ok[v] = true;
	for (auto to : g[v])
		if (!ok[to])
			dfs1(to);
}

void dfs2(int v) {
	used[v] = true;
	++cnt;
	for (auto to : g[v])
		if (!used[to] && !ok[to])
			dfs2(to);
}

int main() {
#ifdef _DEBUG
	freopen("input.txt", "r", stdin);
//	freopen("output.txt", "w", stdout);
#endif
	
	cin >> n >> m >> s;
	--s;
	for (int i = 0; i < m; ++i) {
		int x, y;
		cin >> x >> y;
		--x, --y;
		g[x].push_back(y);
	}
	
	dfs1(s);
	
	vector<pair<int, int>> val;
	for (int i = 0; i < n; ++i) {
		if (!ok[i]) {
			cnt = 0;
			memset(used, false, sizeof(used));
			dfs2(i);
			val.push_back(make_pair(cnt, i));
		}
	}
	sort(val.begin(), val.end());
	reverse(val.begin(), val.end());
	
	int ans = 0;
	for (auto it : val) {
		if (!ok[it.second]) {
			++ans;
			dfs1(it.second);
		}
	}
	
	cout << ans << endl;

	return 0;
}

Линейное решение (Vovuh)

#include <bits/stdc++.h>

using namespace std;

const int N = 5010;

int n, m, s;
vector<int> g[N];
vector<int> tg[N];
vector<int> cg[N];
vector<int> ord;
int indeg[N];
bool ucomp[N];
bool used[N];
int comp[N];
int cnt;

void dfs1(int v) {
	used[v] = true;
	for (auto to : g[v])
		if (!used[to])
			dfs1(to);
	ord.push_back(v);
}

void dfs2(int v) {
	comp[v] = cnt;
	for (auto to : tg[v])
		if (comp[to] == -1)
			dfs2(to);
}

void dfs3(int v) {
	ucomp[v] = true;
	for (auto to : cg[v])
		if (!ucomp[to])
			dfs3(to);
}

int main() {
#ifdef _DEBUG
	freopen("input.txt", "r", stdin);
//	freopen("output.txt", "w", stdout);
#endif
	
	cin >> n >> m >> s;
	--s;
	for (int i = 0; i < m; ++i) {
		int x, y;
		cin >> x >> y;
		--x, --y;
		g[x].push_back(y);
		tg[y].push_back(x);
	}
	
	for (int i = 0; i < n; ++i) {
		if (!used[i]) {
			dfs1(i);
		}
	}
	
	reverse(ord.begin(), ord.end());
	memset(comp, -1, sizeof(comp));
	for (int i = 0; i < n; ++i) {
		if (comp[ord[i]] == -1) {
			dfs2(ord[i]);
			++cnt;
		}
	}
	
	for (int v = 0; v < n; ++v) {
		for (auto to : g[v]) {
			if (comp[v] != comp[to]) {
				cg[comp[v]].push_back(comp[to]);
				++indeg[comp[to]];
			}
		}
	}
	
	dfs3(comp[s]);
	int ans = 0;
	for (int i = 0; i < cnt; ++i)
		if (!ucomp[i] && indeg[i] == 0)
			++ans;
			
	cout << ans << endl;
	
	return 0;
}

999F - Cards and Joy

Разбор

Решение (Vovuh)

#include <bits/stdc++.h>

using namespace std;

const int N = 520;
const int K = 12;
const int C = 100 * 1000 + 11;

int n, k;
int c[C];
int f[C];
vector<int> h;

int dp[N][K * N];

int main() {
#ifdef _DEBUG
	freopen("input.txt", "r", stdin);
//	freopen("output.txt", "w", stdout);
#endif
	
	cin >> n >> k;
	h = vector<int>(k + 1);
	for (int i = 0; i < n * k; ++i) {
		int x;
		cin >> x;
		++c[x];
	}
	for (int i = 0; i < n; ++i) {
		int x;
		cin >> x;
		++f[x];
	}
	for (int i = 1; i <= k; ++i)
		cin >> h[i];
		
	for (int i = 0; i < n; ++i) {
		for (int j = 0; j <= n * k; ++j) {
			for (int cur = 0; cur <= k; ++cur) {
				dp[i + 1][j + cur] = max(dp[i + 1][j + cur], dp[i][j] + h[cur]);
			}
		}
	}
	
	int ans = 0;
	for (int i = 0; i < C; ++i) {
		if (f[i] != 0) ans += dp[f[i]][c[i]];
	}
	
	cout << ans << endl;
	
	return 0;
}

Комментарии (112)

Показать архивные | Написать комментарий?

wallcrawler

6 лет назад, # |

+17

Thanks for the editorial, and interesting problems, surely we get to learn something!!

→ Ответить

Ashik_01

Thanks for the editorial

joaquimnt_

My ideia on 999E - Reachability from the Capital is as follows:

Build a new graph with all contracted SCCs in the original graph.
In the new graph, for each vertex not reachable from scc[s], compute the in degree.
Insert a pair composed of < degree[i], i > into a set and run one DFS per each element.
Each DFS runned means one edge added. In the end, the numbers os DFS executed is the answer.

Great contest! :) 39522069

alagneB_diK

6 лет назад, # ^ |

You don't need DFS for each element in the set, the answer is the number of SCC with 0 in degree. All SCC with > 0 in degree will be reached by some vertex, so it is not good to add edges between the capital and some vertex in a SCC with > 0 in degree.

alwerty

What is D complexity? I think O(2*m + n)

vovuh

O, i wanted to write the time complexity for each of the described solutions and forget about it :( I will do it now :)

Hossam

vovuh, in D if the problem were adjusted so that we can increase/decrease the numbers, can it still have a greedy solution or even DP, It can be solved by Max-flow min-cut but with the constraints adjusted, any idea?

I thought about it right now, with increase\decrease the elements this problem can be solved at least by mincost maxflow (but this is most stupid idea, i will think about it more time and may be i will find better solution)

vovuh please feel free to update me here once you've arrived at something.

kingosak

would anyone provide binary search solution for D as mentioned in tags

I think this would be proper, I'm using std::set though to find the nearest number that has less than n / m numbers to fill from the current number I'm at with numbers > n / m 39484134

Mostly the tags include concepts that can be used, it doesn't mean that their obvious strict implementation is intended but rather the way they work in a certain condition, hope this is clear!

ninetailfox

how should i start practicing for problem D, i am not able to solve them ?? (please don't go with my color).

← Rev. 4 →

How can I judge the Kyubi??

Let's start with the simple facts:

1) numbers themselves aren't important, we only care about their modulus to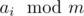 m(i.e. $\text{[math]}$ )

2) count the numbers that have the same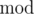 $\text{[math]}$ and store their indices in the original array

3) now iterate from 0 to m - 1(i.e. all possible mods under m) and if you have a mod that has numbers more than k = n / m store them somewhere call is Large, also store the numbers than have less than k = n / m in a set(or any container that supports finding the nearest number) call it Small

4)now for each number in Large in increasing order, call X = count(large[i]) - n / m and you already know the mod of large[i] call it Z, now try to find the nearest mod in Small that is larger than Z in a cyclic order(i.e. if Z = m — 1, then search in[0, Z - 1]) call what you found V and replace the index of this number with any number that have mod = V, do this for all X numbers in large[i].

5) now to the proving part, since the problem tells you that you can only increase the numbers you have a greedy solution, why? because assume you have at index i numbers than are larger than group size k, these numbers have to go to some modulus other than i (preferably near) in the direction from [i + 1, m - 1] then [0, i - 1], so you find the nearest modulus that have count < group size(k) and replace, this way you chose the best for index i now go on with the next and so on, to prove this is optimal, suppose there's another index larger than i with count > group size(k) and you decided to go with it first before finding the answer for i first, now suppose you found the answer for that other index and replaced, now i will still have to move much more steps to reach a valid number with count < group size(k), thus our choice of larger index first was wrong, hence the optimal way is to use modulus in increasing cyclic order.

submission: 39484134

cXs5

Thanks for your proof. But I still have a small quetion. XD

In step 5), why i have to move much more steps to reach a valid number with count < group size(k) if we found the answer for another index larger than i with count > group size(k) and replaced ?

Could you please give me some counterexamples ? :)

N = 8, M = 4, K = 2 0 4 12 1 5 8 9 13 Now numbers wih respect to mod M, are [4, 4, 0, 0] If you solved for $\text{[math]}$ first you'll have to move more steps to solve for $\text{[math]}$

Thanks for your example. XD

In your example, if we sloved for i mod m = 1 first, numbers with respect to mod M are [2, 2, 2(from 1), 2(from 0)], which the total steps are 2 * (2 - 1) + 2 * (3 - 0) = 8. If we sloved for i mod m = 0 first, numbers with respect to mod M are [2, 2, 2(from 0), 2(from 1)], which the total steps are 2 * (2 - 0) + 2 * (3 - 1) = 8, too.

Does this prove that we are correct in using modulus in either increasing or decreasing cyclic order? :)

Looking forward to your reply!

← Rev. 3 →

Ops! Perhaps this example was a bit weak to prove my point, and you can process mods in decreasing direction, as long as you're finding the nearest valid choice in increasing order a(i.e. a mod higher than the one you're currently processing in cyclic order of course), that last example was a proof for that.

Here's a modified version of the counter example The mods array [4, 0, 4, 0] you can process i = 2, 0 in either increasing or decreasing cyclic order, but you cannot replace i = 1, with i = 2, because you now have to go through [2, m - 1] then to [0, 1] which is clearly not optimal.

Got it. Thanks for your detailed explanation! :)

thank you for your detailed solution .

from kyubi.

pratikwankhede

For Question E , Why wouldn't the following solution work?(I'm getting WA):

Answer is the No. of connected components in all the vertices that aren't reachable from s.

First find all the unreachable vertices from s. Find the no. of strongly connected components among the vertices (using all the edges).

Emil_PhysMath

You should find only SCC-s with indegree equal to 0.

Indegree of a Strongly Connected component? Can you explain a little further? Help is appreciated.

← Rev. 2 →

I ment indegree of SCC in the condensed graph(if you don't know the concept fill free to ask). Indegree is number of incoming edges.

To find indegrees of SCC-s we can go through all edges(u->v). If u and v belong to the same SCC then we do nothing. Else we increase indegree of the SCC containing v by 1.

ankit_gupta_

Emil_PhysMath What is the meaning of graph condensation? What are its uses?

Thanks in advance..

Strongly connected component(SCC) is subset of vertices such that any two vertices of this subset are reachable from each other. It is obvious that any vertice belongs to exactly 1 SCC. Thus we can divide the graph into SCC-s. Condensation graph is graph containing every SCC as one vertex. There is an oriented edge between two vertices SCCi and SCCj of the condensation graph if and only if there are two vertices u∈SCCi,v∈SCCj such that there is an edge(u;v) in initial graph. The most important property of the condensation graph is that it is acyclic.

You can read about SCC and condensation graph here.

You are welcome. If you have a question, feel free to ask. :)

shikamaruNARA17

sir i am still unclear with the idea of using SCC , what is wrong in that , if we find the reachable cities
from capital using dfs and then connect other from capital and print the count . i mean just find connected component . i know , i am missing one or two things ,please help

thanks in advance !

My solution

But I can't anderstand your approach.i mean just find connected component you mean to find SCC-s?

P.S. You are welcome :)

Connected component of a directed graph has 2 definitions.

1)SCC.

2)It is weakly connected if it would be connected by ignoring the direction of edges.

If you find number of connected components of type 2 you will not get the right answer.

counter example

4 2 4
1 2
3 2

Your answer would be 1, while the true answer is 2.

Their is no other definition of connected component, if you used some other concept as connected component, please, tell about it in comments.

the_halfbloodprince

sir can you tell me what is wrong with this approach? what i am trying to do is, run a dfs from the capital city and mark all the reachable nodes visited. Now , we again run dfs on those nodes which are not reachable from the capital city but we will not mark this node as visited. Example, if 2 is not reachable from capital city then we will run a dfs from 2 and will mark all the cities reachable from 2 as visited except for 2. And later, lets say 3 is also not reachable from capital city, so we run a dfs on 3 as well and mark all nodes reachable from it as visited except for 3.If 2 ,which was not marked visited initially , is reachable from 3 then 2 will be marked as visited. Finally we run a loop for all nodes and if a node is not visited just increment the final count. below is my solution 39578066

the_halfbloodprince, your program fails on test case below.

input

right answer

your programs output

Here is your mistake: After _dfs-s from nodes 1,2,3 _dfs from node 4 is called. It goes to node 3 which is already visited=>doesn't go to node 2, so node 2 remains unvisited.

I am thinking how to fix it. If I have an idea I'll type it in comments

the_halfbloodprince, you need two arrays visited instead of one. In _dfs function you will use the second array, and before calling _dfs in main() you will have to fill it with value false. And after calling _dfs: if for node u visited2[u]==true you will assign true to visited1[u]: visited1[ind]=true.

like this

for(int i=0;i<n;i++)
    if(!visited1[i])
    {
        for(int ind=0;ind<n;ind++)
            visited2[ind]=false;
        _dfs(graph,visited2,i,i);
        for(int ind=0;ind<n;ind++)
            if(visited2[ind])
                visited1[ind]=true;
    }

39601152. Finally AC!!! :)

Emil_PhysMath Thanks for your answer sir.Now, i got it.

the_halfbloodprince, you are welcome!!!

anctartica

Could you please tell a bit more about solving question E with O(n+m) complexity?

If you are interested, in the third spoiler of the problem is a linear solution to it. You can read more about Strongly Connected Components (SCC) here. Another part of the solution is quite easy i think. If I am wrong feel free to ask me.

Fighter.human

Wouldn't be complexity for this solution is O(n*m) ?? As you are running two loops:

for (int v = 0; v < n; ++v) { for (auto to : g[v]) { if (comp[v] != comp[to]) { cg[comp[v]].push_back(comp[to]); ++indeg[comp[to]]; } } }

At worst case wouldn't it be O(n*m) ?

No, it will not, because of we will iterate over each vertex and each edge of the given graph only once in this two cycles. So the complexity is O(n + m).

raghav0307

In problem E, could anyone show that the solution, explained in second para of the tutorial, will always give an optimal answer.

shouryap

If the number of edges added is less than the number of vertices with indegree 0 in the graph's condensation ( other than the vertex containing the capital), then we will still have a vertex in the condensation with indegree 0 and which does not contain the capital. This vertex is unreachable.

On the other hand, if you add all edges from the capital to such vertices, we can show that any vertex in the condensation is reachable; just "backtrack". Say if you want to reach a vertex u in the condensation, find a vertex v1 such that v1-> u is an edge. Then find v2 such that v2->v1 is an edge. We must terminate somewhere because the graph is a DAG. It can terminate only at a vertex with indegree 0, and this vertex is the vertex containing the capital.

ameya

Any idea why this solution for D fails on test case 8?
I wrote it to mimic the official solution :/

I_D0nt_Kn0w

In problem E , why do we need to again run a dfs according to count? Why does this solution 39525886 gives answer 1 more than the correct answer for the test case no:4? Can someone help me in understanding the incorrectness of my solution? If possible , please explain with a sample graph.

Abhishek-420

4 года назад, # ^ |

i also have same doubt .if you know the solution let me know

Muhammad_mhs

My solution approach for Problem E: First of all , I take topological order of each node. Then, I run DFS from the city and then from the topological order. And answer should number of connected component — 1.

Brankonymous

Can someone explain to me how and WHY this dp solution for F works? I really don't understand O(n^2*k^2) for loop, but I don't understand also ans=(1,10^5)∑ i=dp[f[i]][c[i]] part. I think this way: if I let's say use c[i]=2 cards and k is equal to 3. I need to use my 3rd card that is not my favorite but that instantly means that some other card won't have same amount of c[j]. What am I missing?

OptxPrime

Formal proof for O(n*m) in E? I have intuitive proof but I want to see mathematically precise proof.

sg4ss

for D i tried a different approach which led to the same min no. of changes...but diff array.. but I think the judge is checking only for a particular array...whereas in the question it says print any array..

my code

Ghost0fSparta

No, the minimum changes in testcase 1 is 3 whereas your code outputs 4 which is wrong

sabertooth

I was wondering if there can be a solution for E with DSU
We will count number of Disjoint Unit for ans..?

JustForFun.

I think it can work with dsu ,but when we unite them we need dfs too.

like this 39531065

ram_24

Thanks a lot for nice tutorials:)

← Rev. 5 →

Need help for D problem: I am doing the same approach as in editorial but it is giving wrong answer in testcase 8. Please help.

I think the problem is in updating the array. What I am doing is maintaining a pointer p1(representing remainder) which initially starts from free[0]%m and then moves forward in circular fashion. Whenever I see that p1%m has count < k, I change value free[i] such that free[i]%m = p1%m. Please I cannot find my mistake. Need help.
Code

ACapella

I'm getting a wrong answer on the same test and I applied the approach as in the editorial. did it work out with you?

No man, I couldn't figure it out :(

mykhail0

3 года назад, # ^ |

You can check the possible cause here. Your solution is indeed wrong for the test case I created.

saket21

Help needed understanding problem F, thanks

Single_Ready_To_Mingle

Try to solve this problem first :

Given N persons and M cards, where each person can have atmost K cards, what is the maximum possible value of total joy levels ? The joy level of a person having x cards is H[x].

Example : N = 3 , M = 4 , K = 3

H[0] = 0, H[1] = 2 , H[2] = 6, H[3] = 7

Maximum value of total joy level can be obtained by giving 2 cards to person 1 , 2 cards to person 2 and none to person 3. The ans is 12 (H[2] + H[2] + H[0]) in this case. Note that there exists other possible distribution of cards such that total joy level is 12. Above is just one way.

rr459595

Can someone please explain problem F ? Thanks.

zemotacqy

A very nice contest. In problem E, my approach is the following: I used the concept of Disjoint Set Union. I say 1. whenever (in the input) vertex v (as input) is the capital. OR 2. the root of vertex v (as input) is the capital I don't perform union operation. The answer are the number of vertices whose: root(vertex)==vertex && vertex!=capital

The approach works fine for the sample test cases, I got wrong answer in 4th test case. Please provide some small test cases to try my approach on.

Your program fails on this test case.

Good luck :)

shahidul_brur

For problem E, I got AC by pretty simple implementation, without taking reverse graph, without counting in degree: 39539472

Is my solution correct or the test is weak? Is there any case when my solution will fail ?

My approach is:
1. Mark all the nodes which are reachable from s
2. Run dfs in the original graph and push the nodes in stack according to dfs finishing time.
3. Pop each node from stack and if it is still unvisited run a dfs from here and increase answer by 1.

My code:

#include<bits/stdc++.h>
using namespace std;
vector<int> g[5002];
bool vis[5002];
void dfs(int u)
{
    vis[u]=1;
    for(int v:g[u]) if(!vis[v])
        dfs(v);
}
stack<int> stk;
void dfs2(int u)
{
    vis[u]=1;
    for(int v:g[u]) if(!vis[v])
        dfs(v);
    stk.push(u);
}
int main()
{
    ios_base::sync_with_stdio(0);cin.tie(nullptr);
    //freopen("in.txt", "r", stdin);
    int n, e, s;
    cin>>n>>e>>s;
    for(int i = 1;i<=e;i++)
    {
        int u, v;
        cin>>u>>v;
        g[u].push_back(v);
    }
    dfs(s);
    for(int i = 1;i<=n;i++) 
        if(vis[i]==0) dfs2(i);
    
    memset(vis, 0, sizeof vis);
    int cnt = 0;
    while(!stk.empty())
    {
        int u = stk.top(); stk.pop();
        if(!vis[u])
        {
            cnt++;
            dfs(u);
        }
    }
    cout << cnt;
    return 0;
}

vovuh, can you please take a look ?

Your approach is also correct, I have the same idea as yours and BledDest has proved this solution correctness

Thanks for your reply. What's the proof of the correctness of such solution?

BledDest

In this post adding a vertex means adding a directed edge from s to this vertex.

Suppose that your solution adds some vertex x to the answer and it is a bad move (in the optimal answer you should add some other vertex y such that x is reachable from y). Then there are two cases:

1) y is reachable from x. Then x and y belong to the same SCC, and any vertex that is reachable from x is also reachable from y (and vice versa). So there is no difference between adding x and adding y.

2) y is not reachable from x. Then since you pushed vertices to the stack according to their dfs finishing time, then y will be pushed later than x, and extracted before x. So the solution won't add x to the answer but will instead add y.

Is the proof clear?

ritikesh1999

Could you please explain with an example?

codeflix

But what if the graph is:

n = 3 m = 3

1 -> 2

2 -> 1

1 -> 3

And suppose we are starting our DFS from 1. Ideally node 3(x) should be pushed into the stack before node 2(y). But here it is possible that 3 is pushed after 2. Am is missing something here?

Edit: Found my mistake!

supriyanta

for the problem E why do we need to sort the array which stores the cnt?

devarshi09

Sorting is required because we have to connect the components of the graph greedily!So we need to find the source with maximum connected nodes!

To find the source from which maximum nodes can be reached. This is important because we have to connect the graph greedily!

genius_noob

Isn't it possible that the nodes in sorted order may visit the similar nodes ?

Yes it is .That's why after sorting the nodes we have to run the DFS and convert all the bad nodes into good ones.

What i was asking is let's say if node 1 in sorted order visit 4,5,6 and node 2 visits 5,6,7 and node 3 visits 2, 7. Then the 2nd node will be selected while it is not required. Am i missing something ?

Node 2 won't be selected because according to your example node 3 visits node 2 that means you will run DFS from node 3 before node 2 . DFS from node 3 will convert bad node 2 into good node hence avoid revisit .

for (auto it : val) { if (!ok[it.second]) { ++ans; dfs1(it.second); } } In sorted list, node 2 will come before node 3 as its count is 3. Can you plz explain how node 3 is selected before node 2 ? "according to your example node 3 visits node 2 that mean you will run DFS from node 3 before node 2". How ? I hope you are considering all 1, 2 and 3 as bad nodes.

You need to sort node according to the amount of node you can visit from that node ..in non increasing order In your example we can reach 4 nodes from node 3 but only 3 nodes from node 2 .That means 3 will come before 2.

Oh My bad.I got it. Thanks Buddy.

Yeah :)

vlada851

What is Greedily? And what happens if we don't sort? (I think I understand, but cant delete this message)

Cool!

Tosic

Hello, Could someone tell me what is the formal proof that the solution of problem D is optimal? I know someone has already written some proof but I really can't understand that one. Thanks,

sorablaze_11

My solution for problem E is as follows:

Run a dfs and mark all the nodes visited through s.
Run another dfs and store all the nodes not visited through first dfs in a stack in topological order.
Iterate over the stack and after poping out each node check if visited or not(don't forgot to reinitialize the visited array as 0), if not visited run a dfs and add 1 to answer otherwise continue.

Time Complexity: Linear

Solution

would anyone provide better explanation for F . ps: provide recursive solution if possible

http://codeforces.net/contest/999/submission/39534469

natofp

In E problem is that correct? Count SCC number with 0 indegree and substract 1 from answear if S lies in SCC with 0 indegree?

Yes that works ... informally, when you connect a vertex to an SCC with in-degree 0 (let's call it C), you will be able to reach the maximum number of nodes, because the rest (unreachable from C) is completely disconnected from this SCC, so you'd have to add a new edge anyway, and if you choose to add an edge to an SCC reacahble from C, you won't reach C itself (if you find SCC so that none is a sub-graph of the other, e.g. with Kosaraju's algorithm), and will still have to add a new edge, which will make the previous one redundant.

Bekh

Could somebody please point out to me why I get WA on this solution for 999D - Equalize the Remainders ? 39544753

312352145215

Hi! Your programs fails for example on this test case.

Spoiler

Right answer:

I hope it will help you, good luck :)

Hey! Thanks for your time. I think I fixed this bug by not reversing the 'free' vector, but it still give me WA on test 8. I'm not sure if it actually got fixed for all the cases I don't quite understand the basis on which we find the closest element to increment(I don't understand why the editorial chose to do the adding and removing in the same loop instead of doing it in 2 loops. How does that make the solution optimal?). Here's the submission 39604949

rdd6584

http://codeforces.net/contest/999/submission/39629449 I think the main idea is the same with the editorial.

But I can't understand why my code is incorrect on test case #8. Iterating 10 times output is different from iterating twice.

Would anyone explain why two output is different and my code is wrong. I'm sorry for my bad English.

I solved it. Thank you. (i--;)'s locations was reversed.

amitdu6ey

Can anyone please tell me what is wrong with my logic or implementation for problem E? what I am actually doing is- 1> dfs(capital) and mark all visited nodes as good. 2> now run a bfs(bad-nodes) and put them in priority_queue({degree,node}) 3> take nodes from priority_queue from top and run dfs(node) only if it is bad. here is my implementation

Your mistake is in bfs function

for(ll u : adj[s]){
	if(visited[s])	continue;//it should be v[u]
	if(v[s]) continue;//it should be v[u]
	nei++;
	v[s]=true;//it should be v[u]
	Q.push(u);
}

I fixed your code but it gave TLE on test 11. This is the code 39669926.

thanks! But i think worst case time of my code is ~10^7 i.e n(n+m) + nlog(n) ~ n^2. can you please explain why i am getting TLE

You are welcome! I fixed your code so it gets AC now(39677394). There are 3 main reasons why your code worked slowly.

1)In your bfs function you had map<int,bool> v;. I changed it to bool v[5005];. map works in logarithmic time. Array works in O(1). Never use map, if you can use a simple array.

2)Never use long long type if you don't need to. long long works slower than int.

3)iostream works slowly. Use stdio.

Chocxcoff

For problem C i got this error. Can anyone tell me how to fix it? I'm stuck

This is the error:

wrong answer Unexpected EOF in the participants output

This is my submission: http://codeforces.net/contest/999/submission/39488231

You have used variable temp without initialization. You have to add this line to your code.

temp=0;

But your solution is too slow(it gets TLE on test 4).

In problem E, linear solution, what is the purpose of dfs3() ? In order to avoid source vertex containing SCC having indegree 0, just do indegree [comp[s]] = 1.

majdoor

I have implemented top down approach for 999F,please have a look at my code and tell me where am i going wrong,as i am facing problem in clearing test case 3 http://codeforces.net/contest/999/submission/39853333

OBITO

5 лет назад, # |

why WA https://codeforces.net/contest/999/submission/55944188 problem D

DS007

My alternate solution to E: 1. Generate topological ordering on the graph, first calling dfs on s 3. for vertex v in topo: if (!reached[v]) ans++; dfs(v)(updating reached instead of explored); 4. Print ans

harsha_1_2

In 999E - Reachability from the Capital after we add an edge to a bad vertex shouldn't we be finding the order of bad vertices again. Can someone help me understand how the same order of bad vertices work even after adding an edge?

purp4ever

in problem 999E - Reachability from the Capital: i did a DfS from the capital to connect the good cities and for each bad city i started a DFS and if it reaches a new node or a node marked with 2 it changes it to 1 and when the DFS ends i mark it with 2 and the answer is the number of 2s but it is not running 63881015 can you please explain why it isn't working

aryan12

In Question E, my solution is giving MLE. Could anyone please help me. Link to submission : https://codeforces.net/contest/999/submission/66542471

TopGun__

I did E in O(n) only with two dfs.

NumERATOR

4 года назад, # |

I have an extremely easy solution for problem E with only one very small dfs in O(n) and have a look at my code .. We can also prove its correctness.

https://codeforces.net/contest/999/submission/90504569

zztqwq

My solution for problem E is: Using Tarjan's algorithm to find the graph's strongly connected components and change it to a DAG. Then you will find the answer is the number of points with no in degree. In particular, if in[s]==0, answer--.

3 года назад, # |

This is for everyone who doesn't pass TC 8 for 999D - Equalize the Remainders.

If you solve this without binary search and keep two pointers for remainders under $$$\frac{n}{m}$$$ and for those over it, check if you update the pointers accordingly.

My solution with a bug: 152495726 and here's my solution without a bug: 152500977.

A simpler test case than TC 8, which I thought of, that also points out the bug:

10 5
0 5 10 2 7 12 3 4 9 14

Y'all's solutions usually print 9 as the answer, but the correct answer is 4.

Блог пользователя vovuh