Preliminary, changes to come possibly.
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
| # | User | Rating |
|---|---|---|
| 1 | jiangly | 4039 |
| 2 | tourist | 3841 |
| 3 | jqdai0815 | 3682 |
| 4 | ksun48 | 3590 |
| 5 | ecnerwala | 3542 |
| 6 | Benq | 3535 |
| 7 | orzdevinwang | 3526 |
| 8 | gamegame | 3477 |
| 9 | heuristica | 3357 |
| 10 | Radewoosh | 3355 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 168 |
| 2 | -is-this-fft- | 165 |
| 3 | atcoder_official | 160 |
| 3 | Um_nik | 160 |
| 5 | djm03178 | 158 |
| 6 | Dominater069 | 156 |
| 7 | adamant | 153 |
| 8 | luogu_official | 152 |
| 9 | awoo | 151 |
| 10 | TheScrasse | 147 |
Preliminary, changes to come possibly.
| Name |
|---|



No solutions?
#include <bits/stdc++.h> using namespace std; #define ll long long int int main() { ios::sync_with_stdio(0); cin.tie(0); #ifndef ONLINE_JUDGE // freopen("input1.txt", "r", stdin); // freopen("output.txt", "w", stdout); #endif ll n, sum=0 ; int v[]={100,20,10,5,1}; cin >> n; int i=0; while(n!=0){ sum+=n/v[i]; n%=v[i]; i++; } cout<<sum; return 0; }can you guys write your code in spoiler tags please?
Explain to someone how the solution working for O (n ^ 2) has been tested in task B
I see some of the participants passed Div.1 C by random shuffling and greedy approach. Could anyone explain the rationale behind this solution?
My solution shouldn't have worked but it did. Basically i was taking vectors greedily but because i knew there were countertests, i did so starting from the last vector and going back to the first.
I think creating test cases to break a greedy algorithm is pretty tricky — each vector needs to be roughly orthogonal to the greedy sum of the previous ones, and as soon as one adds some randomisation it's basically impossible to break.
To avoid the use of randomization, the authors may put some constraints like the found solution should be lexicographically smallest by defining -1 < 1 or vice versa.
But at the same time, this would mean that the problem is looking for the unique solution which can be obtained only if the solution is similar to intended solution.
For Div1 F, what is the O(n) interpolation you had in mind? I used Lagrange interpolation in O(n^2), and while I can see how one could optimise that to O(n) by incrementally computing each term from the previous one, it would add a lot of complexity.
Though I don't have the formula on hand, if you write out what Lagrange interpolation gives and then substitute x = D into the formula, it becomes a sum of the dp values times some binomial coefficients. We can do this in O(n) with some preprocessing.
Here is the code: http://codeforces.net/contest/995/submission/39639811
You should post it here if you figure out what it is :P
That's more-or-less what I had in mind, although that code is still O(n^2). It would be pretty easy to make O(n) though by first computing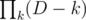 and then using that to get
and then using that to get 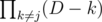 for each j.
for each j.
In problem C-tesla, in the first sample, why am I getting WA cause I put car No 5 in (4, 1) as temp place? I will put it in right place after that.
The problem statement says that a car can only be moved into row 1 or 4 if that is its designated parking spot.
You can't do that. "Furthermore, Allen can only move one of his cars into a space on the first or fourth rows if it is the car's designated parking space."
Rating drop for sure now :/ this was a bad day.
Just now, I wrote something very similar to your solution with E except I used random_shuffle and it passed, you should give it a go.
How did your solution work? We can't choose vectors randomly right?
We choose them greedily
let's say the vector pointing to current position is p
we calculate
p — a[i] and p + a[i]
and choose which one has the smallest distance from (0,0)
Now this is definitely incorrect greedy and there is probably a counter-case, but it is sort of hard to break.
But now, seeing that the process is O(n), I thought if I scrambled it it is unlikely the solution would fail the constraints over a thousand times so I continued to run this process until it passed.
Also note I used "sqnorm" which is just the magnitude squared, becauseI wanted to avoid floating-points and sqrt() function, but I don't think it's necessary.
UPD: Good job on solving :D
Oh , okay . Thank you!
Problem E says "We can show that the answer always exists."
While statistically I'd be very surprised if it didn't, does anyone have an actual proof?
I wanted to ask the same question. Even though I pretty quickly thought of "random" solution which I was sure will pass, I though that authors should have an actual proof to state something like this which would probably be a constructive provable solution.
Well, this graph is called the "Margulis expander". An expander graph is a graph that kind of "expands" optimally in a BFS. There are explicit lower bounds on the expansion using deep number theory.
In other words, yeah I can "prove" the solution works, but not in a way that works in contest. To be honest, I just was feeling experimental with this problem.
LOL. I had exam in university like two weeks ago and large part of that course was about expanders. We had 'Margulis expander' in the course but I found the proof so big and ugly so I didn't even tried to learn it and even forget the what it is about :) Could save me some time on trying to come up with actual solution.
math tasks
for B.would any one explain how the following two codes differ in logic... one is accepted while other is giving TLE.. http://codeforces.net/contest/996/submission/39630623 http://codeforces.net/contest/996/submission/39631431
try using int instead of long long.
why??
Int operation are faster. And I don't know why you are all downvoting preda2or, he's probably right.
For Div2-E, I don't know what is the difference but in the solution I submitted during contest, I processed each vector in the order given and kept changing the position vector through my algorithm which got WA on TC 79. However,after contest I did a slight change and stored all the vectors and then iterated in reverse manner, from n-1 to 0 using the same algo and I got an AC. Can anyone explain to me what is the difference?
It is hard to make good data. Probably the latter solution just gets lucky.
Can you please share the model solution ? Most solutions I’m finding use randomisation.
Even I got WA on TC 79. Did you use the fact that whenever we add a vector we just try to be greedy and hence take that sign which reduces the distances and nothing more? Is there any problem with this approach?
I did the same and I dont know what is wrong with the approach.
Sir, I want to know why that claim is right. If I have two vector, one of them is (5,6) and its length is max, the other is (5,5). But their sum is better than the length of (5,6). So, why that chaim is right?
Sorry, I can understand it now! Thanks!
Problem E. Here is BFS, that finds the answer of length ≤ shortest_path_length + 3. http://codeforces.net/contest/995/submission/39632072
(It's simple bidirectional bfs with used array for buckets of size 4 on bitset),
desert97, the complexity of making an entire circle is actually 2*n, not k.
There are only k cars in the cycle. So advancing k cars by one is O(k).
But at each move, you move into neighbouring empty space which means you move one by one. It's not clearly described though.
The time complexity of it is O(2n) (unless you do it in a clever way), but the number of moves is O(k).
Can anybody give me the source code of Div.2 B no problem with the same approach which has been provided in the editorial?
http://codeforces.net/contest/996/submission/39618290
Does anyone have solution for div1 C as described in editorial (the binary tree and vectors as leaves)
nice Python solution for DIV2 problem B
you can find more like this here: https://codeforces.net/blog/entry/60059
If anyone solved Problem C using dynamic approach please share it. Thank You
My Solution for Div2 .A https://coolforces.blogspot.com/2018/06/996A-Codeforces-Hit-the-lottery-solution.html .B https://coolforces.blogspot.com/2018/06/996b-codeforces-world-cup-solution.html .D https://coolforces.blogspot.com/2018/06/996d-codeforces-suit-and-tie-solution.html
Finding a linear time solution to “suit and tie” is equivalent to counting inversions in and array. As far as I know there is no known exact algorithm for calculating inversions in O(n).
Okay, you're right. So is probably the best we can do.
is probably the best we can do.
How do you reduce counting inversions to suit and tie?
Look at your solution.i got idea of counting inversion from your solution :P
but what is idea behind f[a[i]]<f[a[j]] will add into answer
count how many value already less than f[a[i]] and update it using BIT!!
This is not what I asked. What I am asking is: Given a problem of counting invesions, can we reduce it to an instance of the problem "suit and tie", which is necessary for equivalence.
Consider a permutation of 1 through n, and place 1 2 3 ... n to the left of this array. Then the answer for suit and tie is the same as the number of inversions of the permutation plus n(n-1)/2.
Then the answer for suit and tie is the same as the number of inversions of the permutation plus n(n-1)/2.
I'm sorry but this fact is not obvious to me. Can you please elaborate ?
As in the editorial, we only need to consider for each pair, the relative ordering and add up the number of swaps needde. If a < b, the possible orderings in our sequence is a ... b ... b ... a or a ... b ... a ... b.
In case a b b a there is one inversion in original array and two swaps needed.
In case a b a b there is no inversion in original array and one swap needed.
If you know where everything should go, you can relabel the people to numbers 1..2N. Now, you are asking the question “given a permuation of 2N values, how many adjacent swaps are needed to sort it”.
The general idea is that your array will become sorted when there are 0 inversions left, and that each adjacent pair swap will eliminate (or add, but we don’t want that) 1 inversion. So therefore the number of adjacent swaps needed is equal to the number of inversions.
https://stackoverflow.com/questions/20990127/sorting-a-sequence-by-swapping-adjacent-elements-using-minimum-swaps
Edit: ksun has commented how to turn inversion counting back into the suit and tie problem.
So is the problem equivalent to -
I believe the number of inversions of a permutation can be found in O(n) time. So, is this an O(n) solution ?
The lower bound for counting inversions in a permutation is as of 2010.
as of 2010.
Wait ... What about when you decompose into cycles ?
Am I wrong ?
4 3 2 1The cycles are 1 → 4 → 1, 3 → 2 → 3. Your algorithm will return 2, while the answer is 6.
I understood the mistake. Cycle decomposition counts the parity of the permutation in O(n) time, not the exact number of inversions !
Thanks !
I have a doubt about how to do the relabelling. Can you help me understand how exactly to relabel the integers ? I was thinking every pair but that’s not optimal. Do you need to know the optimal arrangement apriori before reducing it to inversion counting ?
but that’s not optimal. Do you need to know the optimal arrangement apriori before reducing it to inversion counting ?
You can do the relabelling in increasing order. Let the original array be 3 1 2 3 1 2. Relabel 3 as 1 , 1 as 2 and 2 as 3. The transformed array is 1 2 3 1 2 3. Then find the number of inversions in the transformed array.
Code
I did the relabeling in the following manner: a: original array. b: relabeled array.
Great contest ! It met my expectations and the editorial is very well written compared to most CodeForces tutorials.
In Div 2 E, I didn’t understand why two vectors in the same 60 degree segment have sum less than r. Can someone please explain ?
Geometry: If AB < 1, AC < 1 in a triangle, and , then BC < 1. This is because the angle opposite an angle less than 60 cannot be the longest side of the triangle.
, then BC < 1. This is because the angle opposite an angle less than 60 cannot be the longest side of the triangle.
Wow ! Great proof. Should have been included in the editorial !
Can anyone please tell me whats wrong with this code for problem 996B.39614833 . Somebody plz help me
Wrong logic.
Generic comment.
You forgot that he can go many laps around the queues, so after your for loop, if it didn't find any empty queue you can't just output the last queue you must instead let him walk around the queues again and again until he finds an empty queue.
someone plz explain how greedy approach will work for div2 D
If the leftmost person is in pair a, swap the other person in pair a left, to the second position. Now the first two people are both in pair a, and we repeat the process on the remaining n−1 pairs of people recursively.
i am not getting this line :|
Notice that by switching the other person to the left, we will switch everyone between them to the right. We don't want to switch the leftmost pair because there's a chance that some person inbetween the pair will be farther than before
For example this tc: 1 2 3 2 4 1 3 4 -> 1 2 3 2 1 4 3 4 -> 1 2 3 1 2 4 3 4 -> 1 2 1 3 2 4 3 4 -> 1 1 2 3 2 4 3 4 -> 1 1 2 2 3 4 3 4 ....
If we switch the right 1, all other pair won't be farther than before (2 pair distance will be the same, 3 and 4 pair will be closer). But by switching the left 1, the 3 pair and the 4 pair will be farther.
okay got it!!
can u explain me logic behind this solution
http://codeforces.net/contest/995/submission/39620454
For each number(i), we will eventually need a swap with j (j < i) if a[i] leftmost number < a[j] leftmost number
1 2 3 2 4 1 3 4 -> 6th number and 7th number will eventually swap with 5th number, but 5th number won't need to swap with number before it
For problem A, why does this matter? "The solutions works because each number in the sequence 1, 5, 10, 20, 100 is a divisor of the number after it."
Basically, this is a special version of the coin change problem.
In general, this problem cannot be solved by Greedy, and instead you should use Dynamic programming, however if the coin system has certain properties, it can be proved that greedy works. The proof goes as follows for each coin you get the maximum amount you can do, and argue that any larger, it's better to use coin i + 1.
Lets say you have different coins. For instance coins with the values 1, 3, 4. Try to form the value 6 with them. The optimal solution is 3 + 3, while the greedy one gives the worse result 4 + 1 + 1.
I think he asked for a proof of why does greedy algorithm work for that particular denomination and not for an example of how greedy fails.
Yeah that's exactly what I want.
Here's a mathematical proof for it:
Let denote with (a, b, c, d, e) a solution (you take a coins of value 1, b coins of value 5, ...) If you apply the greedy algorithm, then you obviously get a solution with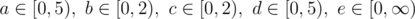 . Also you can convert each such tuple back into its value a·1 + b·5 + c·10 + d·20 + e·100, a non-negative number.
. Also you can convert each such tuple back into its value a·1 + b·5 + c·10 + d·20 + e·100, a non-negative number.
Obviously these two operations form inversions. E.g. if you apply the greedy algorithm on the number x = a·1 + b·5 + c·10 + d·20 + e·100, you will get e coins with value 100, because a·1 + b·5 + c·10 + d·20 ≤ 4·1 + 1·5 + 1·10 + 4·20 = 99. In the same way you get d coins with value 20, since a·1 + b·5 + c·10 ≤ 4·1 + 1·5 + 1·10 = 19. And so on.
So the greedy approach is a bijective function between [0, ∞) and [0, 5) × [0, 2) × [0, 2) × [0, 5) × [0, ∞).
Now, assume you have an optimal solution (a, b, c, d, e) for some x, that is not identical to the greedy solution. Because the greedy approach is a bijection, the solution cannot be in [0, 5) × [0, 2) × [0, 2) × [0, 5) × [0, ∞). Therefore either a ≥ 5, b ≥ 2, c ≥ 2 or d ≥ 5. In either case we can replace some coins and get an even better solution. Therefore we have a contradiction, which means that the greedy solution is always optimal.
Very nice proof. Thanks. For denominations where one of them is not a divisor of the next, we cannot have such bounds for a,b,c,d,e, so greedy solution may or may not work for such cases right ?
Yes, you can't find bounds that will form a bijection.
You can still use greedy exchange though.
This videa has nice proof starting at 9:30 and only takes about 10 minutes.
I think in editorial for 996 B the condition k+tn>=ak is not correct because on first step nothing is decreased so it should be k+tn>ak.
We start indexation since 0.
" (Maybe it can be even done in O(n), anyone?)."
This is regarding div-2 D. Can anyone please link me an O(n) solution? desert97
It seems it is not possible http://codeforces.net/blog/entry/60217?#comment-440367 But maybe in O(n sqrt(logn)) http://codeforces.net/blog/entry/60217?#comment-440466
Thanks :)
Isn't it too easy for coding when you have the idea of the problems? Div1 DEF can all be solved in 50-60 lines(maybe less) . I think a good contest should also focus on the implement difficulty.
I think div1 A was for implement difficulty.
E, F can be solved in 50-60 lines?
How did this bruteforce approach for Div-2 B get accepted ? Code : http://codeforces.net/contest/996/submission/39628778
I’m very surprised ! Explain your approach please.
div1F , a much simpler solution is to just calculate dpi = number of ways to assign i distinct numbers to the tree nodes , then answer is just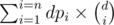 .
.
rajat1603 can you explain how dp[i] is calculated? I am also confused on how to calculate D choose i for large D values efficiently.
EDIT: I'm good with the D choose i part, since i is at most 3000.
dp1i = the number of ways of assigning numbers ≤ i to tree [just the solution to the original problem] , this can be calculated as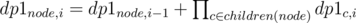 .
.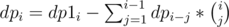 .
.
now to calculate dpi = number of ways of assigning exact i distinct numbers to tree , we can use the formula
I don't get how this is the solution to original problem.
Can anyone please explain Div-2E(Div-1C) — Leaving the Bar? I have read the editorial but unable to understand anything. I can't visualize the solution described in the editorial and can't relate the editorial with the problem statement.
Thanks in advance.
I have tried my best here. Let me know if it helps.
Thank you for your proofs.
great explanation!!!
basel-99 USACOW The solutions works because each number in the sequence 1,5,10,20,100 is a divisor of the number after it.
Here are my solutions to the problems of this contest.
I found Div2 E/ Div 1 C a very different question. So, I tried my best to explain it here with the help of the editorial here.
Here's my editorial to Div 2 D/ Div 1 D
For the Div. 1 E problem, what would be a rough value of the probability for Solution 1? I don't find the probability of an "intersection" very high. Could you please show how to do the calculations? Thanks.
I did weird implementation of Suit and Tie of O(n sqr.) complexity:
http://codeforces.net/contest/996/submission/39659575
Happy Coding
Can someone direct me to the idea of Lagrange Interpolation? I understand the general idea of it, but how do you put it to work in div1F?
Given n+1 points, Lagrange interpolation lets you find the polynomial of degree bound n which passes through all the given points. Basically we define a polynomial f(x), which gives us the answer for d=x. Now, we calculate the first n+1 integer values of this polynomial via dynamic programming (f(0) through f(n)), and then use Lagrange interpolation to find the polynomial f(x) (which has degree bound n as per lemma in editorial), and then evaluate the polynomial, at f(d), to get the answer.
mmmm and since Lagrange interpolation is the only unique solution at the lowest degree this fit. First of all thanks, I got the idea now because of that :) Maybe you also know why the lemma is correct? it has a maximum of x(x-1)(x-2)...(x-n) I guess because it will always use "d choose n" at max. Although this is true, how can you know this beforehand...?
Never the less, this does make the code writing very simple...
Let P(x, a) denote the no of possible labellings for the subtree rooted at node n, and the label of node a equals to x. Now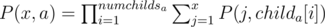
You can show that prefix sum of any polynomial on integers will have degree 1 higher than the polynomial itself (relate on the lines of sum of kth powers of first n natural numbers).
Let ss[i] denote the subtree size of node i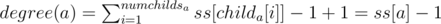
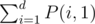 which'll have degree ss[1] = n
which'll have degree ss[1] = n
To make induction work, we assume for now that the degree of polynomial for every child i of node a was ss[i] - 1. Hence,
The base case for this induction will be the leaf nodes, where P(x, a) = 1 and thus the assumption is valid. Hence, our induction holds.
Now, the final answer will be
But why the complexity of the interpolation is O(n) mentioned in the tutorial? I think the normal Lagrange interpolation is O(n2). I don't really get the point.
desert97 if div2C tesla had asked about the minimum number of moves to park all the cars, I guess rotating the circle wouldn't have been a good strategy. Any idea on how could we find it?
I doubt it's possible in polynomial time. Might even be possible to show it's NP-hard.
can you post links to your solutions desert97
Can someone please disscuss the Binary indexed tree approach for Suit and Tie Ques
You can just simulate the process from the editorial. Let's say that the sequence looks like this:
abc....ab...c.... First we want to bring the secondanext to the first one. This takes|number of elements between a and a|steps. Then you want to bring the secondbnext to the first one. This takes|number of elements between b and b without the a-s|steps, because the secondais already to the left of the firstb(if we simulate the process). And so on.To solve this with BIT. Initialize the bit with an array of 1s. For each letter you to
range_sumsteps, and afterwards you delete the two elements by setting them to 0.I'm sure that there are multiple approaches.
For problem Div 2E / 1C editorial : Any two points in this sector will have distance at most r. How to prove this ?
See this, or you can prove it with cosine theorem.
If div2 — 995C leaving the bar — if I greedily take every vector's sign so that it reduces the distance from the origin than this approach shows WA on TC79. What is wrong with this approach?
My submission — #39620913
Try this :
Draw the figure on paper and you'll know the greedy approach is wrong. You may want to see the discuss above.
In Div2.F / Div1.D , how can we get (v_i,0+v_i,1)/2=E_f by induction ? I tried some ways including induction, but failed. Can someone please explain it ?
According to the solution of problem B, shouldn´t the result for test case n = 3 and {5, 5, 5} be 2? Since for the first gate, you can write 1 + 3*2 = 7 > 5, for the second one 2 + 3*1 = 5, and for the third one 3 + 3*1 = 6 > 5. Can someone explain to me why is the answer 3?
I'm not sure why it says >= in the editorial when I think it should just be >. In your example, there are 5 people in each of the queues so the queues are only available starting at minute 6. So for each i you find the minimum t such that k + t*n > a[k] instead of >= a[k].
For div2.E/div1.C, I implemented in a tricky way like this.
I wonder if this can be proved to be correct and if not, how to hack it.
Can someone please elaborate the euclidean algorithm solution to E? Thanks!
First, since all operations are reversible, we can just get u and v to some common number (which is 1 in this case).
Let (a,b) represent the number a*b^(-1) modulo p (for v != 0). Then, we can see the following operations:
This is similar to the euclidean algorithm (we do the first operation if a > b, otherwise we do operation 2, until we get to (gcd(a,b), gcd(a,b))).
Of course, this might not be very fast for (u,1), but we can instead do it with (u*x mod p, x) for some x!=0, which is an equivalent state. The claim without proof is that for random x, it is likely this will take < 100 steps (not sure why this is true either).
Thanks for the clear explanation!
I tried the gcd approach, however picking a single random x does not seem to work, but it does work for small enough number of attempts with different values of x to get an AC verdict. The submission is 39734619. Am I missing something here?
How the problem 996A Hit The Lottery can be solved using dp ? Please help if anyone knows.
Not really.. Considering the fact that n <**=** 10^9;
Hi
I was trying Problem C Tesla.
I have written this code which gives Time Limit Exceeded on test case 6.
http://codeforces.net/contest/996/submission/39723591
I am rotating the cars clockwise.
Can anyone tell me why is my program taking so much time? I think it is O(n^2). How do I reduce running time?
can someone please explain the initial dp used in F?
let f[i][j] = the answer of the i-th subtree and the max salary won't exceed j . Then f[i][j] = f[i][j-1] + π(f[son[i]][j]) where π means the product of all things involved in the brace .
In div2-E, div1-C
39809949
39809939
I don't know why first code is wrong but second is right. Difference is just for-loop 0 to n -> for-loop n-1 to -1. why? why second is right??
How about testcase like below
3
600000 -600000
0 999999
1000000 0
When input this testcase, first code output 1 1 -1, so p = (-40000, 399999) and second code output -1 1 1, so p = (40000, 1599999).
It is hard to design data to break all solutions in this problem. The second one just got lucky.
Oh, i know that make all-round testcase is hard.
Anyway, I'm glad it's a tastcase-problem ... I thought there was something else I did not know about. Thx!
I had seen some people's solution of Problem C. And some of the code are wrong when I input test case below: 3 600000 -600000 0 999999 1000000 0
In Leaving the Bar problem, how can we be sure that it is always possible to construct a circle through any 3 points of some radius r with origin as the center?
Of Div.1 C, what is the probability to pass a worst case performing $$$k$$$ times random_shuffle and greedy algorithm?